|
Further number sequences part I |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Number sequences - 6 to 8 |
|
Workout |
|
57 slides |
|
| Further number sequences |
|
Library |
|
0 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - TASK 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
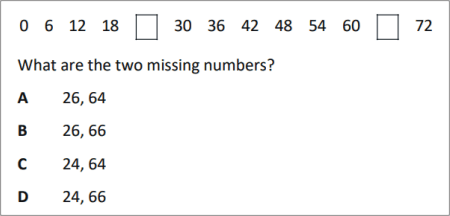 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Counting up in 6s
|
|
312.1 |
|
|
Counting up and down in 6s
|
|
312.3 |
|
|
Times table
|
|
312.4 |
|
|
6 times table
|
|
312.4 |
|
|
Remainder on division by 6
|
|
312.6 |
|
|
Number bond sum to 6
|
|
312.8 |
|
|
Communtativity (implicit concept order invariance)
|
|
313.0 |
|
|
Counting up in 6s from any number
|
|
313.2 |
|
|
Counting down in 6s from any number
|
|
313.4 |
|
|
7 times table
|
|
313.6 |
|
|
Counting up and down in 7s
|
|
313.8 |
|
|
Divisibility by 7
|
|
313.9 |
|
|
Remainder on division by 7
|
|
314.1 |
|
|
Number bond sum to 7
|
|
314.3 |
|
|
Sequences in 7s from any number
|
|
314.5 |
|
|
Division of 10 by 7
|
|
314.7 |
|
|
Two and multifactor operations with 7s
|
|
314.9 |
|
|
Sequences with two rules
|
|
315.1 |
|
|
Number puzzels with factors
|
|
315.3 |
|
|
Number puzzels with several operators
|
|
315.5 |
|
|
Mapping diagram
|
|
315.7 |
|
|
8 times table
|
|
315.7 |
|
|
Couting up and down in 8s
|
|
315.9 |
|
|
Whole division by 8
|
|
316.0 |
|
|
Remainder on division by 8
|
|
316.2 |
|
|
Number bond sum to 8
|
|
316.4 |
|
|
Sequences in 8s from any number
|
|
316.6 |
|
|
Indefinite repetition of sequence modulo 8
|
|
316.8 |
|
|
Odd and even cycles. Partition of cycles.
|
|
316.9 |
|
|
Investigation (implicit idea of trying out)
|
|
317.0 |
|
|
Two and multifactor operations with 8s
|
|
317.1 |
|
|
Counting down in 8s
|
|
317.2 |
|
|
Number puzzles involving 8s
|
|
317.3 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
| SLIDE 1
Complete the following sequence up to .
You are going up 6 at a time.
SLIDE 2
SLIDE 3
Count up and down in sixes. Go up to 72 and go back down again.
Use the preceding slide if you need to see the numbers.
SLIDE 4
Complete the following
(a) (e)
(b) (f)
(c) (g)
(d) (h)
SLIDE 5
(a) (e)
(b) (f)
(c) (g)
(d) (h)
SLIDE 6
What is the remainder when the following numbers are divided by 6?
(a) 25 (f) 49
(b) 38 (g) 57
(c) 54 (h) 81
(d) 11 (i) 100
(e) 70 (j) 144
SLIDE 7
(a) (f)
(b) (g)
(c) (h)
(d) (i)
(e) (j)
SLIDE 8
Find every combination of two numbers that add up to 6.
SLIDE 9
Pairs of numbers summing to 6.
And in reverse:
SLIDE 10
Someone once said,
“If I add three numbers in a different order, then the sums are not the same. For example, is not the same as , and is also not the same number.”
Is this statement true or false?
SLIDE 11
“If I add three numbers in a different order, then the sums are not the same. For example, is not the same as , and is also not the same number.”
This statement is false.
The order in which you add any numbers never makes any difference to the total sum.
SLIDE 12
Continue the sequences
?
?
?
SLIDE 13
?
?
?
SLIDE 14
Continue the sequences
?
?
?
SLIDE 15
?
?
?
SLIDE 16
Complete the following sequence up to .
You are going up 7 at a time.
SLIDE 17
SLIDE 18
Count up and down in sevens. Go up to 84 and go back down again.
Use the preceding slide if you need to see the numbers.
SLIDE 19
How many times does 7 go into the following numbers?
(a) 77 (b) 49 (c) 35
(d) 28 (e) 84 (f) 21
(g) 14 (h) 42 (i) 56
(k) 15 (l) 0 (m) 63
SLIDE 20
(a) 77 ? 11 (b) 49 ? 7 (c) 35 ? 5
(d) 28 ? 4 (e) 84 ? 12 (f) 21 ? 3
(g) 14 ? 2 (h) 42 ? 6 (i) 56 ? 8
(k) 15 ? it does not (l) 0 ? 0, zero (m) 63 ? 9
SLIDE 21
What is the remainder when the following numbers are divided by 7?
(a) 36 (f) 49
(b) 51 (g) 27
(c) 54 (h) 81
(d) 74 (i) 101
(e) 65 (j) 145
SLIDE 22
(a) (f)
(b) (g)
(c) (h)
(d) (i)
(e) (j)
SLIDE 23
Find every combination of two numbers that add up to 7.
SLIDE 24
SLIDE 25
Continue the sequences
?
?
SLIDE 26
?
?
SLIDE 27
Someone once said, “When you keep adding 7 every digit between 0 and 9 appears at the end of the numbers in the sequence, and the same sequence of ten digits repeats itself for ever and ever.”
Is this statement true?
SLIDE 28
“When you keep adding 7 every digit between 0 and 9 appears at the end of the numbers in the sequence, and the same sequence of ten digits repeats itself for ever and ever.”
This statement is true.
For example, in the sequence
the final digits are
Every digit appears once and only once in each cycle, and the cycle repeats after the tenth number.
SLIDE 29
Work out the following
(a) (b)
(c) (d)
(e) (f)
SLIDE 30
(a) (b)
(c) (d)
(e) (f)
SLIDE 31
Continue the sequences
?
?
?
SLIDE 32
?
?
?
SLIDE 33
? How can I make the number 15 using the digits 3 and 5?
? How can I make the number 24 using the digits 3 and 8?
? How can I make the number 56 using the digits 2, 4 and 7?
SLIDE 34
? . Multiply 3 and 5.
? . Multiply 3 and 8.
? . Multiply 2, 4 and 7 altogether.
SLIDE 35
? How can I make the number 24 using 3, 3, 8, 8?
? How can I make the number 24 using 3, 3, 5?
? How can I make the number 24 using 4, 4, 7?
SLIDE 36
? How can I make the number 24 using 3, 3, 8, 8?
. Add 3, 3, 8 and 8 together.
? How can I make the number 24 using 3, 3, 5?
Add 3 and 5 together. Then, multiply the result by 3.
? How can I make the number 24 using 4, 4, 7?
Multiply 7 and 4 together. Then, subtract 4 from the result.
SLIDE 37
Complete the following sequence.
SLIDE 38
SLIDE 39
Count up and down in eights. Go up to 96 and go back down again.
Use the preceding slide if you need to see the numbers.
SLIDE 40
How many times does 8 go into the following numbers?
(a) 24 (f) 32
(b) 96 (g) 56
(c) 40 (h) 64
(d) 16 (i) 88
(e) 48 (j) 104
SLIDE 41
(a) (f)
(b) (g)
(c) (h)
(d) (i)
(e) (j)
SLIDE 42
What is the remainder when the following numbers are divided by 8?
(a) 41 (f) 37
(b) 51 (g) 43
(c) 61 (h) 67
(d) 71 (i) 101
(e) 81 (j) 160
SLIDE 43
(a) (f)
(b) (g)
(c) (h)
(d) (i)
(e) (j)
SLIDE 44
Find every combination of two numbers that add up to 8.
SLIDE 45
SLIDE 46
Continue the sequences
?
?
SLIDE 47
?
?
SLIDE 48
When you add 8 to a number the final digit of the new number is 2 less than the final digit of the first number.
For example, when I add 8 to 28, the new number is 36. The final digit of the new number is 6, which is 2 less than the final digit of the first number, 8.
This means that when we add 8 repeatedly to an even number we get an endless repeat of the cycle
And with an odd number
Explain why this is true.
SLIDE 49
8 is 2 less than 10. So, when we add 8 to a number, we first add 10 and then subtract 2. Adding 10 leaves the final digit unchanged, and subtracting 2 reduces the final digit by 2.
So, when adding 8, the final digits go in the cycles
Even
Odd
SLIDE 50
When adding 8, the final digits go in the cycles
Even
Odd
Investigate the cycles made when we add by 6 and 7
SLIDE 51
Adding 6
Even
Odd
There is one cycle for the even numbers, and another for the odd numbers.
Adding 7
There is only one cycle, and every digit from 0 to 9 appears once this cycle.
SLIDE 52
Work out the following
(a) (d)
(b) (e)
(c) (f)
SLIDE 53
SLIDE 54
Continue the sequences
?
?
?
SLIDE 55
?
?
?
SLIDE 56
? How can I make the number 59 using 3, 7 and 8?
? How can I make the number 9 using 3, 5, 6 and 8?
? How can I make the number 5 using 2, 56 and 8?
SLIDE 57
? . Multiply 7 and 8 and then add 3.
? .
Multiply 6 and 8. Subtract 3. Then divide by 9.
? . Divide 56 by 8. Subtract 2.
|
|