|
Combinations |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| More than one way |
|
Workout |
|
53 slides |
|
| Combinations |
|
Library |
|
15 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Combination (implicit)
|
|
412.1 |
|
|
Different ways
|
|
412.5 |
|
|
Permutation, arrangement
|
|
412.7 |
|
|
Permutations of three symbols
|
|
412.9 |
|
|
Permutations of four symbols
|
|
413.3 |
|
|
Place-value
|
|
413.5 |
|
|
Number represented by digits
|
|
413.8 |
|
|
Denary system
|
|
414.0 |
|
|
Binary system
|
|
414.2 |
|
|
Binary addition
|
|
415.3 |
|
|
Traffic cone question
|
|
415.7 |
|
|
Probability and permutations
|
|
415.5 |
|
|
Problems involving permutations of n-digit numbers
|
|
416.0 |
|
|
Dirichlet pigeon-hole principle (implicit)
|
|
416.2 |
|
|
Knight move in chess
|
|
416.6 |
|
|
Network
|
|
416.8 |
|
|
Shortest path in a network
|
|
416.8 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
Find all the ways of making 60 pence using only 20 pence and 10 pence coins.
Complete the table
Number of 20p coins Number of 10p coins Sum
3 0 20p + 20p + 20p = 60p
SLIDE 2
Number of 20p coins Number of 10p coins Sum
3 0 20p + 20p + 20p = 60p
2 2 20p + 20p + 10p + 10p = 60p
1 4
0 6
SLIDE 1 B
Find all the ways of making 50 cents using only 25 cent, 10 cent and 5 cent coins. Complete the table.
Number of 25¢ coins Number of 10¢ coins Number of 5¢ coins Sum
2 0 0 25¢ + 25¢
SLIDE 2 B
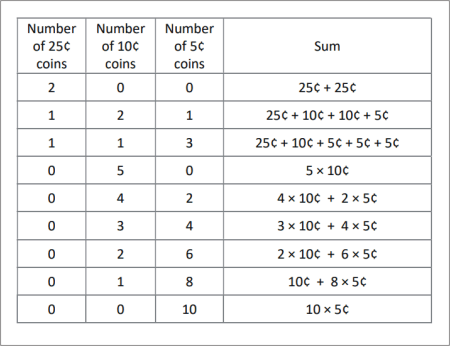
Number of 25¢ coins Number of 10¢ coins Number of 5¢ coins Sum
2 0 0 25¢ + 25¢
1 2 1 25¢ + 10¢ + 10¢ + 5¢
1 1 3 25¢ + 10¢ + 5¢ + 5¢ + 5¢
0 5 0 5 × 10¢
0 4 2 4 × 10¢ + 2 × 5¢
0 3 4 3 × 10¢ + 4 × 5¢
0 2 6 2 × 10¢ + 6 × 5¢
0 1 8 10¢ + 8 × 5¢
0 0 10 10 × 5¢
SLIDE 3
Work out every possible total that can be made with one 5p, one 2p and one 1p coin using three, two or one coins
SLIDE 4
5p 2p 1p Sum Coins
1 1 1
3
1 1 0
2
1 0 1
2
1 0 0
1
0 1 1
2
0 1 0
1
0 0 1
1
SLIDE 3B
Work out every possible total that can be made with one 10¢, one 5¢ and one 1¢ coin using three, two or one coins.
SLIDE 4B
10¢ 5¢ 1¢ Sum Coins
1 1 1
3
1 1 0
2
1 0 1
2
1 0 0
1
0 1 1
2
0 1 0
1
0 0 1
1
SLIDE 5
The sum of 8p can be made with 5p, 2p and 1p coins in seven different ways.
Complete the table to show all of these.
Number of 5p coins Number of 2p coins Number of 1p coins
1 1 1
SLIDE 6
Number of 5p coins Number of 2p coins Number of 1p coins
1 1 1
1 0 3
0 1 6
0 2 4
0 3 2
0 4 0
0 0 8
SLIDE 5B
The sum of 20¢ can be made with 10¢, 5¢ and 1¢ coins in seven different ways.
Complete the table to show all of these.
Number of 10¢ coins Number of 5¢ coins Number of 1¢ coins
2 0 0
SLIDE 6B
Number of 10¢ coins Number of 5¢ coins Number of 1¢ coins
2 0 0
1 2 0
1 1 5
0 4 0
0 3 5
0 2 10
0 1 15
0 0 20
SLIDE 7
Two cards from a pack of cards are chosen.
These cards can be arranged in two different ways
We count these as different arrangements
There are six different arrangements of three different cards
Find all six arrangements
Such arrangements are also called permutations
SLIDE 8
SLIDE 9
Find all the permutations of the letters
A B C
SLIDE 10
A B C B A C C A B
A C B B C A C B A
possibilities
This is exactly the same question as the previous question, only using letters A B C instead of playing cards.
Tutor note
The permutations of three objects is a standard problem, and one that the student is required to solve with any three different items.
SLIDE 11
Find all possible arrangements of the numbers
1 2 3
SLIDE 12
1 2 3 2 1 3 3 1 2
1 3 2 2 3 1 3 2 1
This is exactly the same question as the previous question, only using the numbers 1 2 3 instead of the letters A B C.
SLIDE 13
Find all the permutations of the letters
A B C D
SLIDE 14
A B C D B A C D C A B D D A B C
A B D C B A D C C A D B D A C B
A C B D B C A D C B A D D B A C
A C D B B C D A C B D A D B C A
A D B C B D A C C D A B D C A B
A D C B B D C A C D B A D C B A
There are permutations
SLIDE 15
The meaning of the number 4578.63 is found from the place-value of each of its digits.
digit place-value number
4 1000 4000
5 100 500
7 10 70
8 1 8 units
6
4
SLIDE 16
Complete the following for the number 392.547
digit place-value number
3
9
2
5
4
7
SLIDE 17
digit place-value number
3 100 300
9 10 90
2 1 2 units
5
4
7
SLIDE 18
A number is represented by a series of digits in which each digit takes the value from 0 to 9
Complete the following
?
?
SLIDE 19
?
?
SLIDE 20
We represent numbers using digits
In the denary system we use the digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
There are ten digits. In counting, when we get to ten items, instead of inventing a new digit, we start over. Twelve is represented by the digits 12 where the place-value of the first 1 is ten and the place-value of the 2 is two units.
? How many units does the 3 in 325 represent?
? How many units does the 6 in 876 represent?
? How many units does the 0 in 302 represent?
SLIDE 21
? In 325 the 3 represents three hundred units
? In 876 the 6 represents six units
? The 0 in 302 represents zero tens of units
SLIDE 22
In the binary system we have only two digits, 0 and 1
When we add 1 to 1 in the denary system, we get 2, but in the binary system we start over with a new digit
The first four binary numbers
binary denary
0 0
1 1
10 2
11 3
? Complete the following
denary binary
? The binary for the number four is 100. Complete the following
binary denary
100 4
101
6
111
? What is binary for the number eight?
SLIDE 23
? denary binary
? The binary for the number four is 100. Complete the following
binary denary
100 4
101 5
110 6
111 7
? Binary for 8 is 1000.
SLIDE 24
binary denary power of 2 exponent
0 0
0
10
1
100
2
1000 8
10000
100000
1000000 64 6
SLIDE 25
binary denary power of 2 exponent
0 0
0
10 2
1
100 4
2
1000 8
3
10000 16
4
100000 32
5
1000000 64
6
SLIDE 26
Convert the following numbers from binary to denary
? 1011
? 1100
? 10101
? 110001
? 101110
SLIDE 27
?
?
?
?
?
SLIDE 28
Write the following denary numbers in binary
? 9
? 13
? 27
? 32
? 47
SLIDE 29
?
?
?
?
?
SLIDE 30
Convert the following sums in denary into binary sums
?
?
?
?
?
SLIDE 31
?
?
?
?
?
SLIDE 32
Complete the following
SLIDE 33
SLIDE 34
When the machine finishes turning each box can contain only one of the three pictures
? Give three different arrangements (permutations) of the three pictures
? How many different permutations are there altogether?
? You win if you have three smiley faces
If each permutation is equally likely, what is the probability of your winning?
SLIDE 35
? There are twenty-seven possible solutions. For example
? There are 3 options for the first box, 3 for the second and 3 for the third.
permutations in all
? Only one way of winning in 27 equally likely outcomes.
Probability
SLIDE 36
There are six policemen standing between traffic cones along a street while a parade passes by. If each policeman is standing between two traffic cones, how many traffic cones are there?
SLIDE 37
The traffic cone question
Let ?be a cone, and ?be a policeman
?????????????
There are six policemen but seven traffic cones
In such questions there is one more boundary than there is box
SLIDE 38
A chessboard has eight by eight squares, or sixty-four squares in all. How many lines are required to draw a chessboard?
SLIDE 39
There are eight squares in a row by nine edges. Same for the columns.
lines are required to draw a chessboard.
SLIDE 40
? A raffle ticket contains a 4-digit number. This number cannot begin with a zero. Only one ticket will be picked to win the prize. What is the probability of winning the prize?
? A telephone book contains 5-digit numbers not beginning with a 0 or 1, and not ending in a 0. How many possible telephone numbers are there?
SLIDE 41
? A raffle ticket contains a 4-digit number. This number cannot begin with a zero. Only one ticket will be picked to win the prize. What is the probability of winning the prize?
There are 9000 numbers between 1000 and 9999
Probability
? A telephone book contains 5-digit numbers not beginning with a 0 or 1, and not ending in a 0. How many possible telephone numbers are there?
There are 8 ways of picking the first digit, 10 ways of picking the second digit, 10 ways of picking the third digit, 10 ways of picking the fourth digit and 9 ways of picking the last digit.
SLIDE 42
A class contains 13 students. Why must two of these students have a birthday in the same month?
SLIDE 43
A class contains 13 students. Why must two of these students have a birthday in the same month?
Solution
There are 12 months in a year, but here there are 13 students. Suppose 12 of these students have birthdays in different months. Then the last student must have a birthday in the a month that is the same as one of the other students.
Note
This is an application of the Dirichlet pigeon-hole principle. For example, you cannot fit seven pigeons into six pigeon-holes.
SLIDE 44
A chessboard has sixty-four squares. Two squares are removed as shown in diagram A, leaving sixty-two squares.
You have 31 domino pieces, as shown in the diagram. You are instructed to cover the sixty-two squares of the board so that the dark side of the domino covers a dark square on the board, and the light side covers a white square. In figure 2 two domino pieces have been placed on the board.
Is it possible to do this? Explain your answer.
SLIDE 45
A chessboard has sixty-four squares. Two squares are removed as shown in diagram A, leaving sixty-two squares.
You have 31 domino pieces, as shown in the diagram. You are instructed to cover the sixty-two squares of the board so that the dark side of the domino covers a dark square on the board, and the light side covers a white square. In figure 2 two domino pieces have been placed on the board.
Is it possible to do this? Explain your answer.
This is not possible. The two squares that have been removed from the chessboard are both white squares. There are 32 dark squares and 30 white squares, but in the collection of 31 dominos there are 31 dark squares and 31 light squares. So the board cannot be covered in this way.
SLIDE 46
The diagram shows how a knight in chess can move.
Find all the squares that a knight could move to in one and two moves from the square shown in the diagram.
SLIDE 47
SLIDE 48
The diagram shows a network of roads between four towns with distances in miles.
Find all the possible ways of going from A to D and the length of these routes. Which route is the shortest?
SLIDE 49
Route ABD Length
Route AD Length 31 miles
Route ACD Length
Shortest route: ACD
SLIDE 50
The diagram shows a network of roads between four towns with distances in miles.
Find all the possible ways of going from A to E and the length of these routes. Which route is the shortest?
SLIDE 51
Route ABE Length
Route ADE Length
Route ACE Length
Route ADCE Length
Route ACDE Length
Shortest route: ADCE
SLIDE 52
The diagram shows a network of roads between four towns with distances in miles.
Find all the possible ways of going from A to E and the length of these routes. Which route is the shortest?
SLIDE 53
Route ABE Length
Route ADE Length
Route ACE Length
Route ADBE Length
Route ABDE Length
Route ADCE Length
Route ACDE Length
There are two shortest routes: ADE and ABDE
|
|