|
Working in three dimensions |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Volumes and projections |
|
Workout |
|
61 slides |
|
| Volumes and projections |
|
Library |
|
17 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
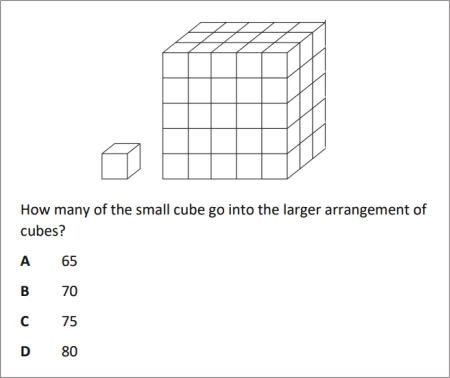 |
|
SOLUTION |
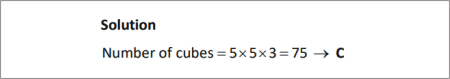 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Array
|
|
486.1 |
|
|
Assemblage of cubes
|
|
486.1 |
|
|
Assemblage of objects
|
|
486.3 |
|
|
Cuboid
|
|
486.7 |
|
|
Volume of cuboid
|
|
486.7 |
|
|
Breadth
|
|
486.7 |
|
|
Packing problem
|
|
486.9 |
|
|
Composite volume
|
|
487.3 |
|
|
Triangular prism
|
|
487.7 |
|
|
Base height formula
|
|
487.7 |
|
|
Volume of triangular prism
|
|
487.7 |
|
|
Square pyramid
|
|
488.5 |
|
|
Volume of square pyramid
|
|
488.5 |
|
|
Net for a cuboid
|
|
488.9 |
|
|
Matching numbers / pairs
|
|
489.1 |
|
|
Plan (architectural)
|
|
489.5 |
|
|
Elevation, front and side
|
|
489.5 |
|
|
Isometric drawing
|
|
489.7 |
|
|
Vertex, edge, face
|
|
490.5 |
|
|
V ‚Äď E + F (Euler's formula)
|
|
490.6 |
|
|
Rectangular prism = cuboid
|
|
490.8 |
|
|
Euler characteristic
|
|
491.0 |
|
|
Triangular prism
|
|
491.2 |
|
|
Pentagonal prism, polygonal prism
|
|
491.2 |
|
|
Octahedron
|
|
491.6 |
|
|
Triangular bipyramid
|
|
491.8 |
|
|
Invariant quantity (Euler characteristic)
|
|
492.0 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 7
Volume of a cuboid is
Units of volume: for example, cubic centimetres, written
Find the volume of this cuboid whose length is 60 cm, width is 30 cm and height is 40 cm
Note: the width of an object is also called its breadth
SLIDE 8
cuboid dimensions: length 60 cm, width 30 cm, height 40 cm
SLIDE 9
At a packing company small boxes each containing a lightbulb are to be packed into large cartons.
The small box is a cube of dimension 10 cm
The carton is a cuboid of dimensions 80 cm by 40 cm by 50 cm
How many small boxes can be packed into one carton?
SLIDE 10
Note that we cancel down before multiplying. This is easier and more efficient.
SLIDE 11
Small boxes are to be packed into a large carton
The small box is a cuboid of dimensions
The carton is a cuboid of dimensions
How many small boxes can be packed into one carton?
SLIDE 12
SLIDE 13
The dimensions of a building are given in the above diagram
Find the total volume of the building
SLIDE 14
The building is made of two cuboids
SLIDE 15
The diagram shows an arrangement of three display cabinets in a department store
Find the total volume of the display cabinets
SLIDE 16
The display is made of three cuboids
The height of the second cuboid is
SLIDE 17
The diagram shows a triangular prism
The triangular base of the prism is a triangle with base 6 cm and height 4 cm
The height of the flat face of the prism is 10 cm
The volume of the prism is the product of the area of the triangular base and its height
Find the volume of the prism
SLIDE 18
SLIDE 19
Find the volume of the prism
SLIDE 20
SLIDE 21
Find the volume of the prism
SLIDE 22
SLIDE 23
Find the volume of the building
SLIDE 24
The building is made of a triangular prism and a cuboid
SLIDE 25
Find the volume of the pyramid
SLIDE 26
SLIDE 27
An ornamental pillar comprises a square column surmounted by a square pyramid
Find the total volume of the pillar
SLIDE 28
The column is a cuboid
SLIDE 29
Three-dimensional objects can be constructed from a net
The illustrations shows how to construct a cube from a net
Using a ruler and compass draw net to construct a cuboid of dimensions
SLIDE 30
SLIDE 31
Put numbers onto the blank faces of this net of a cube so that the numbers on opposite faces add up to 7
SLIDE 32
SLIDE 33
Which of the above could be the net of a cube?
SLIDE 34
B is the net of a cube. All the other diagrams would result when folded in overlapping faces.
SLIDE 35
Draw the plan, the front and side elevations for the following building. The height of the building is 11 m. The roof is a triangular prism, where the triangle is isosceles (symmetric).
SLIDE 36
SLIDE 37
Isometric drawing
SLIDE 38
SLIDE 39
SLIDE 40
SLIDE 41
The numbers indicate the number of cubes high the object is. Make the isometric drawing.
SLIDE 42
SLIDE 43
A building is based on a cube unit.
The diagram shows the plan, back and side elevation of the building. There is a second storey. Number of cubes in the design is shown.
Make an isometric drawing of the building.
SLIDE 44
SLIDE 45
Find the number of vertices, edges and faces of a cube
SLIDE 46
8 vertices, 12 edges and 6 faces
Find for the cube
SLIDE 47
A cube has 8 vertices, 12 edges and 6 faces
SLIDE 48
A cuboid is also called a rectangular prism
? Find the number of vertices (V), edges (E) and faces (F) of a rectangular prism
? Does this differ from V, E and F for a cube?
? What is for a rectangular prism?
SLIDE 49
? V = vertices E = edges F = faces
For a rectangular prism
? Cube and rectangular prism have the same number of vertices, edges and faces
? For a rectangular prism as for a cube
SLIDE 50
V = vertices E = edges F = faces
The formula is called Eulerís formula
The number is called Eulerís characteristic
Find, V, E and F and Eulerís characteristic, , for
? a triangular pyramid
? a square pyramid
SLIDE 51
? triangular pyramid
? square pyramid
SLIDE 52
Find, V, E and F and Eulerís characteristic, , for
? a triangular prism
? a pentagonal prism
SLIDE 53
? triangular prism
? pentagonal prism
SLIDE 54
We can make a hexagonal prism by adding one face to a pentagonal prism.
? Find V, E, F and for the pentagonal prism
? Find V, E, F and for the hexagonal prism
? When one face is added, by how much are V, E and F each increased?
? How has changed when we add one face?
SLIDE 55
We can make a hexagonal prism by adding one face to a pentagonal prism.
? Pentagonal prism
? Hexagonal prism
? When one face is added V is increased by 2, E is increased by 3 and F is increased by 1
? The change when one face is added is
There is no change in the Euler characteristic. Adding one face does not change
SLIDE 56
An octahedron can be made by joining two rectangular pyramids.
? Find V, E, F and for two rectangular pyramids.
? Find V, E, F and for the octahedron.
? When two rectangular pyramids are joined two faces disappear, four vertices are identified, and four edges are identified. By how much are V, E and F each decreased for the two pyramids altogether?
? Subtract the numbers from ? from the numbers from ?. Compare these with the numbers from ?
SLIDE 57
An octahedron can be made by joining two rectangular pyramids
? Two rectangular pyramids
? Octahedron
? When two rectangular pyramids are joined two faces disappear, four vertices are identified, and four edges are identified. We decrease by
? When subtract the numbers from ? from the numbers from ?
We get V, E and F for the octagon, the numbers in ?
SLIDE 58
A trigonal bipyramid is made when two triangular pyramids are joined.
? What is the Euler characteristic of each trigonal pyramid?
? Find V, E, F and for the trigonal bipyramid.
? What is the Euler characteristic of two triangular pyramids combined?
? By gluing two faces together, we remove two faces. How does the Euler characteristic change when two faces are removed by joining them?
SLIDE 59
A trigonal bipyramid is made when two triangular pyramids are joined.
? For each trigonal pyramid
? For the trigonal bipyramid
? The Euler characteristic of two triangular pyramids combined is
? Joining two pyramids doubles the Euler characteristic to 4. But gluing two faces together removes two faces, so the overall Euler characteristic goes down by 2 from 4 to . The Euler characteristic is not changed when two faces are joined.
SLIDE 60
An invariant is a number that does not change
The Euler characteristic is
In both the above cases the Euler characteristic is not changed. In the case of every solid we have considered the Euler characteristic is , regardless of how many vertices, edges and faces we have.
Do you think the Euler characteristic is an invariant?
SLIDE 61
We have not proven that the Euler characteristic is invariant, but the arguments of the previous slides lend considerable support to the claim that the Euler characteristic is invariant.
In fact, we can prove that the Euler characteristic is invariant.
The idea that the Euler characteristic is invariant was proposed by Swiss mathematician Leonhard Euler (1707 Ė 1783). He did not prove it, but it was proven by Augustin-Louis Cauchy (1789 Ė 1857) in 1811.
|
|