|
Working with space |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Space and scale |
|
Workout |
|
66 slides |
|
| Space and scale |
|
Library |
|
-1 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - SUFACE AREA |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.9] |
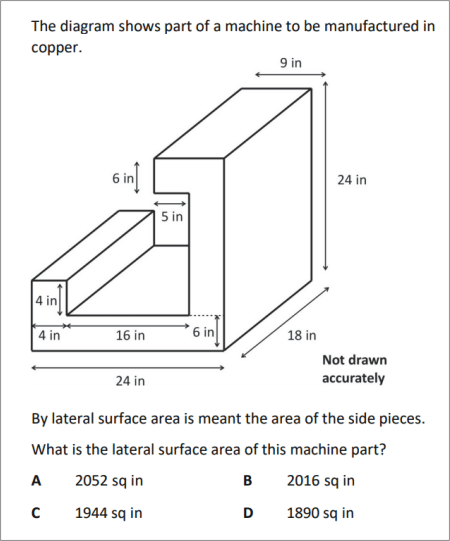 |
|
SOLUTION |
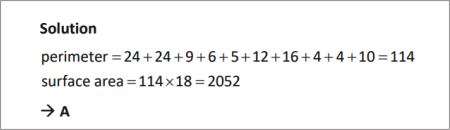 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Optimal spatial arrangement
|
|
554.1 |
|
|
Surface area
|
|
548.1 |
|
|
Lateral
|
|
548.2 |
|
|
Cross-section
|
|
548.3 |
|
|
Wedge
|
|
548.5 |
|
|
Area of circle
|
|
548.7 |
|
|
Pi / π
|
|
548.8 |
|
|
Approximations for pi / π
|
|
548.9 |
|
|
Composite area problems with circles
|
|
549.0 |
|
|
Cylinder
|
|
549.4 |
|
|
Volume of cylinder
|
|
549.5 |
|
|
Bore / hole / pipe
|
|
549.6 |
|
|
Interior / exterior cylinder
|
|
549.7 |
|
|
Cone
|
|
549.8 |
|
|
Volume of cone
|
|
549.9 |
|
|
Equal volume problem
|
|
550.2 |
|
|
Circumference = 2 π r
|
|
550.4 |
|
|
Lateral surface area of a cylinder
|
|
550.6 |
|
|
Composite surface area problem
|
|
550.8 |
|
|
Density
|
|
551.2 |
|
|
Denisty of a mixture problem
|
|
551.9 |
|
|
Scale drawing
|
|
552.1 |
|
|
Map scale
|
|
552.3 |
|
|
Error bound in distance using a map
|
|
552.5 |
|
|
Error bound in density question
|
|
552.7 |
|
|
Ratio of areas
|
|
552.9 |
|
|
Ratio of surface areas
|
|
553.3 |
|
|
Ratio of volumes
|
|
553.4 |
|
|
Isometric scale drawing
|
|
553.7 |
|
|
Axonometric projection
|
|
553.9 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
A martial-arts class uses a hall which is a rectangle 39 m by 23 m. Marcel needs to work out the optimal arrangement of participants in his class. Each participant requires a space of m width facing Marcel by 4 m depth from Marcel. This includes the space needed to separate them. There must be a gap between the wall and each participant of 2 m. Marcel also needs a space of 4 m by 2 m at one end of the class where he can demonstrate the movements, but he can work next to a wall. What is the maximum number of people Marcel can have in his class?
SLIDE 2
There are two possible arrangements and we must decide which is optimal.
The dimensions of the hall are reduced by the 2 m perimeter. Then there is the question of where to place Marcel. The space required by a single participant marked X in each case facing Marcel. This raises the question of whether the areas to the side of Marcel are usable or not. These are marked in dark grey. If they cannot be used, the additional wastage of space in A is 32 m2 and in B 92 m2.
For A we can fit a depth of 6 students ( remainder 1) and a width facing Marcel of just 2 m, since we can only fit 7 m into 19 m twice. Hence, we can only fit 12 students using arrangement A. We cannot increase that by using the wasted space. For B we can fit 5 students across and 3 down, making 15 students. So, arrangement B is better.
Can the 92 m2 of wasted space for B can be better utilized? Further quick sketching to “play” with the arrangement shows that this space cannot be used to improve the fit. (The next best fit is 14 students with 4 facing Marcel, 2 on either side.)
SLIDE 3
A hall is 22 m by 30 m. This hall is to be used for the invigilation of an architectural exam, which requires a large drawing board for each candidate. An area for the invigilators of the exam is required on a raised platform that is 10 m by 4 m. This must be placed at along one wall of the hall. There must be a space of 4 m between this platform and the nearest desk. No desk is to be placed either behind or to the side of the platform. The space for each desk together with its seat is 2 m width by 4 m depth. There must be aisles for the invigilators to walk up and down of width 3 m. Each chair must be separated from any desk in front by 1 m. Work out the maximum number of people who can be invigilated in this hall.
SLIDE 4
The need for 4 m between the platform and the nearest desk increases the size of the platform area to 18 m width and 8 m depth. Arranging the platform along the long wall wastes too much space; a better solution is found by putting it along the short wall. That reduces the space of the hall that can be used to a square 22 m by 22 m. Desks can go along the side of a wall, so the number of aisles is one less than the number of rows of the desks. Including the space between desks each desk takes a space facing the platform of 2 m width by 5 m depth. The optimal solution is 5 rows of desks and 4 aisles, using exactly 22 m width of the hall. We can fit 4 rows of desks depth wise into the 22 m, with 2 m wasted. Answer . The other arrangement gives a maximum of 12.
SLIDE 5
The figure shows a wooden block. All dimensions are in cm. Find the volume and total surface area of the block.
SLIDE 6
The volume is the area of the cross-section the depth. To find the area of the cross-section we could divide it into three pieces and sum those together, but it is quicker (and more instructive) to see this area in terms of one rectangle being removed from another.
The area of the cross-section is therefore . The volume is this multiplied by the depth.
For the surface area we must add the area of the sides to the ends—the ends are equal in area to the cross-section we have just calculated. For the sides, which include the groove cut into the block below, we could add up the areas of all the parts, but it is quicker to find the perimeter of the cross-section and multiply that by the depth.
The perimeter is: 5 + 9 + 5 + 3 + 2.5 + 3 + 2.5 + 3 = 33 cm
The lateral surface area is
The total surface area is
SLIDE 7
The diagram shows the cross-section of a steel girder. All the dimensions are in cm. The length of the girder is 20 m. Find its volume in cubic metres.
SLIDE 8
Cross-section
Volume
SLIDE 9
Find the volume of the wedge. All dimensions are in cm.
SLIDE 10
We need to know the height of the wedge (which is also a prism). This is found by Pythagoras’s theorem. Denoting the height by x, as in the diagram, we find, by Pythagoras
Cross-sectional area (parallelogram)
Volume
SLIDE 11
Area of a circle
The area of a circle with radius r is given by
where is a constant.
The number
An irrational number is one that cannot be written as a fraction. All square roots of prime numbers are irrational numbers. is another irrational number.
The proof that is irrational is beyond the scope of this chapter. (It is post-graduate work.)
Question
What kind of decimal expansion does have?
SLIDE 12
Since is an irrational number, it has a non-recurring decimal expansion.
has been calculated to 31.4 trillion decimal places. There is no regular pattern in the expansion whatsoever, and the expansion of is often used as a random number generator.
SLIDE 13
Approximations for
Since is an irrational number, in practical terms we must approximate it.
Various approximations are used.
? Your calculator will have a stored value of , accurate to a large number of decimal places. For example,
You use this value whenever you use the calculator in a question involving .
? The 3 decimal place approximation to is
This is quite easy to remember, and sufficient for most practical purposes.
? In the old days, when we lived in caves and worked with stones and did not have calculators, we used
The fraction to 3 decimal places, so it is a quite accurate approximation and can still be used when a calculator is not available.
SLIDE 14
The diagram shows two identical circles drawn inside a rectangle of length 28 cm. Find the area of the shaded part. Use .
SLIDE 15
The height of the rectangle is 14 cm and the radius of the circles is 7 cm. The area of one circle is . The shaded area is the area of the rectangle less twice this number.
.
SLIDE 16
A target used in a firing range is made up of three concentric circles of radius 1 cm, 2 cm and 3 cm respectively. Find the ratio of the areas of the shaded regions in the diagram.
SLIDE 17
SLIDE 18
The volume of a cylinder is
where r is the radius of the circular base, and h is the height.
Question
Find the volumes of the following cylinders, giving your answer to 3 significant figures. All measurements are in cm. Use the button on your calculator or take
?
?
SLIDE 19
?
?
SLIDE 20
The diagram shows a copper pipe. The outside diameter of the pipe is 2.5 cm. The diameter of the bore (the hole inside the pipe) is 1.9 cm. The length of the pipe is 80 cm. Find the volume of the copper metal in the pipe, giving your answer to 3 sf.
SLIDE 21
The volume of the copper metal is the volume of the exterior cylinder less the volume of the interior cylinder.
Here diameters have been given. The radius is half the diameter.
For the exterior cylinder
For the interior cylinder
SLIDE 22
The volume of a cone is
Find the volume of a cone whose radius is 5.5 cm and height is 12.2 cm, giving your answer to 3 significant figures.
SLIDE 23
SLIDE 24
The total height of this column, including the cone, is 1.3 m. The diameter of the base is 0.8 m. The height of the cylindrical part is 0.9 m.
Find the volume of the column.
SLIDE 25
Radius =
Height of cone
Volume of cone
Volume of cylinder
Total volume
SLIDE 26
A cube has side 12 cm. Find the radius of the cylinder that has the same volume as the cube, given that the height of the cylinder is also 12 cm.
SLIDE 27
Volume of cube
The volume of cylinder is equal to this
SLIDE 28
The circumference of a circle is where r is the radius.
Since the diameter of a circle is twice its radius, this can also be written where d is the diameter.
? Find the circumference of a circle whose diameter is 14 cm.
? Find the radius of a circle whose circumference is the same as the perimeter of a square with side 7.5 cm.
? Find the circumference of a circle whose area is . Give your answer in terms of .
SLIDE 29
? Find the circumference of a circle whose diameter is 14 cm
? Find the radius of a circle whose circumference is the same as the perimeter of a square with side 7.5 cm.
Perimeter of the square
? Find the circumference of a circle whose area is . Give your answer in terms of .
SLIDE 30
A cylinder can be made from a single flat sheet of material.
The lateral surface area of a cylinder is
where r is the radius of the cylinder and h is its height.
Question
Find the lateral surface area of a cylinder whose radius is 3.2 cm and height is 5.8 cm.
SLIDE 31
Find the lateral surface area of a cylinder whose radius is 3.2 cm and height is 5.8 cm.
SLIDE 32
Find the total area of metal required to make a can that can contain 2 m3 of oil, given that its height is 64 cm.
SLIDE 33
Find the total area of metal required to make a can that can contain 2 m3 of oil, given that its height is 64 cm.
We must consider not only the lateral surface area but the area of the two circles making the top and bottom of the can.
Given that the volume is 2 m3 and the height 0.64 m
Surface area is
SLIDE 34
The diagram shows a case for a part in a machine. The outer part is a semicircle of diameter 15 cm. The thickness of the case is 2.5 cm. The length of the case is 20 cm. Find the total surface area of all six surfaces of the case.
SLIDE 35
The outer part of the case is a semicircle of diameter 15 cm. The thickness of the case is 2.5 cm. The length of the case is 20 cm.
The case comprises two semi-circular “horseshoe” sections, two lateral surfaces and two rectangular end sections.
The diameter of the inner circle is
Two end sections
Side sections
Two rectangular end sections
SLIDE 36
Density
The idea of how much mass there is in a given volume
Example
A nugget of silver of volume 2.53 cm3 has a mass of 26.5 g. Find the density of silver giving your answer to 3 significant figures.
Solution
SLIDE 37
In these questions, give your answers to 2 significant figures.
? A gold bar has a mass of 8.4 kg. The density of gold is 9.3 gcm-3. Work out the volume of the gold bar.
? A block of iron is a cuboid . The density of iron is . What is the mass of the block of iron?
SLIDE 38
? A gold bar has a mass of 8.4 kg. The density of gold is 9.3 gcm-3. Work out the volume of the gold bar.
? A block of iron is a cuboid . The density of iron is . What is the mass of the block of iron?
SLIDE 39
The diagram shows a wooden block. The block has a mass of 450 g. What is the density of the wood used in the block? Give your answer in to 2 significant figures.
SLIDE 40
The block has a mass of 450 g.
SLIDE 41
? The mass of some concrete is . The concrete has density . Find the volume of the concrete.
? This volume of concrete is poured into a concrete pillar to be used to support a bridge, which is a column of constant radius 0.5 m. Find the height of the column, giving your answer to 2 sf.
SLIDE 42
? The mass of some concrete is . The concrete has density . Find the volume of the concrete.
? This volume of concrete is poured into a concrete pillar to be used to support a bridge, which is a column of constant radius 0.5 m. Find the height of the column, giving your answer to 2 sf.
SLIDE 43
The density of some syrup is 1.5 grams per cm3. The density of some carbonated water is 0.98 grams per cm3.
50 cm3 of the carbonated water is mixed with 25 cm3 of the syrup. What is the density of the mixture?
SLIDE 44 – correction of removal of a space added
The density of some syrup is 1.5 grams per cm3. The density of some carbonated water is 0.98 grams per cm3. 50 cm3 of the carbonated water is mixed with 25 cm3 of the syrup. What is the density of the mixture? Give your answer to 3 sf.
SLIDE 45
The diagram shows a scale drawing of a tennis court. The scale of the drawing is . Find the dimensions of the tennis court in metres to 3 sf.
SLIDE 46
The diagram sows a scale drawing of a tennis court. The scale of the drawing is . Find the dimensions of the tennis court in metres to 3 sf.
Solution
Multiply both dimensions by 200
SLIDE 47
On a map, the distance between towns A and B is measured to be 9.4 cm. The scale is . What is the actual distance, in kilometres, between A and B?
SLIDE 48
SLIDE 49
The scale of this map is .
The distance measured between London and Paris, as the crow flies, is 8.6 cm to the nearest 0.1 cm.
What is the lowest and greatest actual distance in km between London and Paris? Give your answer as an error bound.
SLIDE 50
SLIDE 51
A block of wood in the shape of a cuboid is measured to be
Each measurement is accurate to the nearest 1 mm.
The mass of the block of wood is measured to be 2200 g to the nearest 10 g.
What is the least and greatest density of the wood? Give your answer as an error bound to 3 significant figures.
By considering the error bound, state the density of the block of wood to an appropriate degree of accuracy with an error bound.
SLIDE 52
A block of wood in the shape of a cuboid is measured to be
. Each measurement is accurate to the nearest 1 mm. The mass of the block of wood is measured to be 2200 g to the nearest 10 g. What is the least and greatest density of the wood? Give your answer as an error bound to 3 significant figures. By considering the error bound, state the density of the block of wood to an appropriate degree of accuracy with an error bound.
Solution
SLIDE 53
There are three squares. Their sides are in the ratio . Find the ratio of their areas.
SLIDE 54
Ratio of sides
Ratio of areas
SLIDE 55
The radii of three circles are in the ratio . Find the ratio of their areas.
SLIDE 56
Ratio of sides
Since the area of a circle is the ratio of the areas of a circle are the same as the ratio of squares of the sides. (The area is proportional to the square of the side: .)
Ratio of areas
SLIDE 57
The sides of two cubes are in the ratio .
? Find the ratio of their surface areas
? Find the ratio of their volumes.
SLIDE 58
The sides of two cubes are in the ratio .
? Surface area of 1
Surface area of 2
Ratio of surface area of 1 : surface area of 2
? Volume of 1
Volume of 2
Ratio of volume of 1 : volume of 2
SLIDE 59
We have two cubes, A and B. The surface area of B is nine times the surface area of A. What is the ratio of the volume of A to B?
SLIDE 60
The surface area of B is nine times the surface area of A.
If the side of B is 3 units, then the side of A is 1 unit.
Then, the volume of A is 1 cubic unit, and the volume of B is 27 cubic units.
volume A : volume B
SLIDE 61
Onto the isometric grid below make a scale drawing of the building with the above plan and elevations.
SLIDE 62
SLIDE 63
It is possible to have two different angles to represent a building. Make a axonometric projection of the building whose plans and elevations are above. The drawing has been started for you.
SLIDE 63
SLIDE 64
Make a axonometric projection of the building whose plans and elevations are above.
|
|