|
Further work with ratio |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Multiple ratio problems |
|
Workout |
|
23 slides |
|
| Multiple ratio problems |
|
Library |
|
11 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
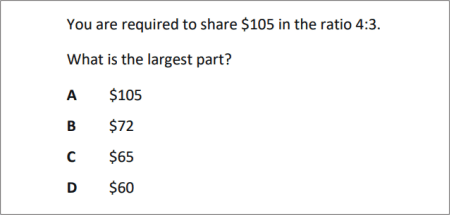 |
|
SOLUTION |
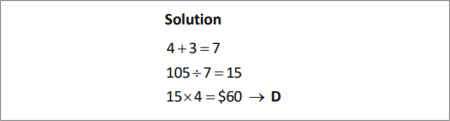 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Multiple ratio problem
|
|
555.7 |
|
|
Tablulating information
|
|
555.7 |
|
|
Flashing lamp problem
|
|
559.2 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
Revision
? Divide £1500 in the ratio
? Richard and Stephen shared a sum of money in the ratio . Stephen received £22 more than Richard. How much money did they share?
SLIDE 2
? Divide £1500 in the ratio
? Richard and Stephen shared a sum of money in the ratio . Stephen received £22 more than Richard. How much money did they share?
Stephen receives parts more than Richard.
SLIDE 1B
Revision
? Divide $1500 in the ratio
? Richard and Stephen shared a sum of money in the ratio . Stephen received $22 more than Richard. How much money did they share?
SLIDE 2B
? Divide $1500 in the ratio
? Richard and Stephen shared a sum of money in the ratio . Stephen received $22 more than Richard. How much money did they share?
Stephen receives parts more than Richard.
SLIDE 3
Revision
At a festival, policemen are lining the road. Between every two policemen there are three traffic cones, and there are policemen at the start and end of the road. If there are 102 traffic cones, how many policemen are there?
SLIDE 4
At a festival, policemen are lining the road. Between every two policemen there are three traffic cones, and there are policemen at the start and end of the road. If there are 102 traffic cones, how many policemen are there?
Solution
There are intervals in which there are cones, with two policemen standing either side. But there is one more policeman than intervals, so policemen in all.
SLIDE 5
Revision
The lowest common multiple of two numbers is the smallest number into which both the numbers divide.
When two numbers are relatively prime the LCM is just the product of the two numbers.
Find the LCM of each of the following
? 14, 35 ? 3, 5, 7
? 4, 10 ? 5, 25, 125
SLIDE 6
?
?
?
?
SLIDE 7
Multiple ratio problems
Example
In a box there are only blue, yellow and red counters. The ratio of the number of blue counters to the number of yellow counters is . The ratio of the number of yellow counters to the number of red counters is . What is the least number of counters in the box? If there are less than 100 counters in the box, what is the greatest possible number of red counters in the box?
Solution
We begin by tabulating the information in the problem
blue yellow red
2 5
4 1
The problem is to combine the two separate ratios into a single ratio of all three coloured counters. This is the same as finding the lowest common multiple (LCM) of the middle term, here the ratio of the yellow counters; this is . We multiply the other ratios accordingly.
blue yellow red
2 5
4 1
8 20 5
We have . The total is 33, which is the minimum number of counters in the box. Since there are less than 100 counters, the maximum number is 99; the greatest number of red counters is 15.
SLIDE 8
At an animal shelter the number of cats to the number of dogs is in the ratio . The ratio of the number of dogs to hedgehogs is . There are 50 hedgehogs at the animal shelter. How many cats are there at the animal shelter?
SLIDE 9
At an animal shelter the number of cats to the number of dogs is in the ratio . The ratio of the number of dogs to hedgehogs is . There are 50 hedgehogs at the animal shelter. How many cats are there at the animal shelter?
Solution
cats dogs hedgehogs
4 1
8 5
32 8 5
320 80 50
There are 320 cats.
SLIDE 10
At a farm, the ratio of the number of horses to donkeys is . At the same farm, the number of donkeys to the number of mules is in the ratio . There are 50 mules at the farm. How many horses are there at the farm?
SLIDE 11
At a farm, the ratio of the number of horses to donkeys is . At the same farm, the number of donkeys to the number of mules is in the ratio . There are 50 mules at the farm. How many horses are there at the farm?
Solution
horses donkeys mules
7 4
8 5
28 16 10
140 80 50
There are 140 horses at the farm.
SLIDE 12
In a bag there are red, white, and black discs. of the discs are red. of the discs are white. What is the smallest possible number of black discs in the bag?
SLIDE 13
In a bag there are red, white, and black discs. of the discs are red. of the discs are white. What is the smallest possible number of black discs in the bag?
Solution
Since of the discs are red and are white,
are black
red white black
3 2 7
The smallest number of black discs is 7.
SLIDE 14
There are 400 marbles in a box. The marbles are either blue, red or green. of the marbles are blue. of the marbles are red. How many green marbles are in the box?
SLIDE 15
There are 400 marbles in a box. The marbles are either blue, red or green. of the marbles are blue. of the marbles are red. How many green marbles are in the box?
Solution
blue red green total
13 4 3 20
260 80 60 400
There are 60 green marbles in the box.
SLIDE 16
A store had 8420 customers on one day. of the customers were locals. of the customers were not locals but came from the same country. The rest were tourists from other country. How many of the customers were tourists?
SLIDE 17
A store had 8420 customers on one day. of the customers were locals. of the customers were not locals but came from the same country. The rest were tourists from other country. How many of the customers were tourists?
Solution
local county tourist total
11 4 5 20
4631 1684 2105 8420
SLIDE 18
A game uses white and black pieces. Some of the shapes are circles, and all the other shapes are squares. The ratio of the number of white shapes to black shapes is . The ratio of the number of white circles to white squares is . The ratio of the number of black circles to the number of black squares is . What fraction of all the shapes are circles?
Hint. Start with the ration of white circles to white squares, and arrange the data in a table.
SLIDE 19
A game uses white and black pieces. Some of the shapes are circles, and all the other shapes are squares. The ratio of the number of white shapes to black shapes is . The ratio of the number of white circles to white squares is . The ratio of the number of black circles to the number of black squares is . What fraction of all the shapes are circles?
Solution
Pick the middle of these ratios and sum them.
White Black
Circle 8
Square 7
15
Since , this gives black shapes as . Then, since we divide 35 in the ratio . This uses all the information, and provides a solution
White Black
Circle 8 10 18
Square 7 25 32
15 35 50
The fraction that are circles is
SLIDE 20
One day, a long time ago, some adults and some children went to Buffalo Billís Wild West Show. The ratio of the number of adults to children was . Each of these spectators had a seat either at the Ringside or in the Gallery. of the children had seats at the Ringside. 117 children had seats in the Gallery. The arena had exactly 2600 seats in all. On this day what fraction of the total seats available were occupied?
SLIDE 21
One day, a long time ago, some adults and some children went to Buffalo Billís Wild West Show. The ratio of the number of adults to children was . Each of these spectators had a seat either at the Ringside or in the Gallery. of the children had seats at the Ringside. 117 children had seats in the Gallery. The arena had exactly 2600 seats in all. On this day what fraction of the total seats available were occupied?
Solution
Begin by putting the information in a table. The ratios are shown in brackets, and the numbers are actual numbers of children or adults
Adults Children Total
Ringside (3)
Gallery 117 (1)
(5) (2) max 2600
Since the children are in the ratio, this gives children at the ringside, and 468 children in all; that gives adults. There is not enough information to find the division of the adults between the ringside and the gallery.
Adults Children Total
Ringside 351
Gallery 117
1170 468 1638 of max 2600
The show is full.
SLIDE 22
Three lamps are flashing. Lamp A flashes every 20 seconds. Lamp B flashes every 45 seconds. Lamp C flashes every 120 seconds. All three lamps start flashing at the same time. How many times in one hour will all three lamps flash at the same time? Count both the first flash at the 0th minute and the last flash at the 60th minute as in the hour.
SLIDE 23
Three lamps are flashing. Lamp A flashes every 20 seconds. Lamp B flashes every 45 seconds. Lamp C flashes every 120 seconds. All three lamps start flashing at the same time. How many times in one hour will all three lamps flash at the same time? Count both the first flash and the last flash as in the hour.
Solution
We must find a number into which both 45 and 120 divide; this LCM is 360 seconds, or 6 minutes. That is, every 6 minutes the lamps all flash together. Including both the 0 minute and the 60 minute they flash together 11 times in one hour.
|
|