|
Modulus |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Size and magnitude |
|
Workout |
|
30 slides |
|
| Modulus |
|
Library |
|
13 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.3] |
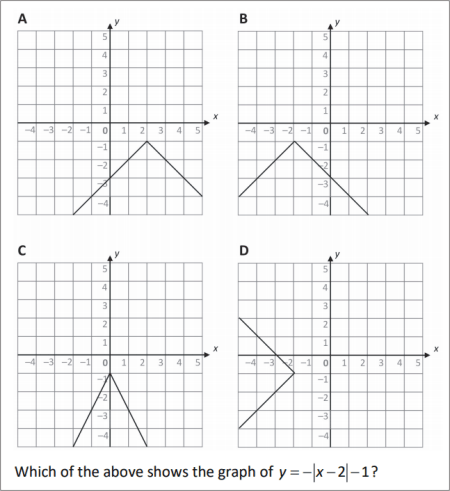 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Size, magnitude
|
|
814.5 |
|
|
Modulus function
|
|
814.5 |
|
|
Definition of modulus
|
|
814.6 |
|
|
Piecewise definition
|
|
814.6 |
|
|
Finding the modulus
|
|
814.7 |
|
|
Graph of modulus function, y = | x |
|
|
814.9 |
|
|
Scalings and vertical translations of modulus
|
|
815.1 |
|
|
Horizontal translation of modulus
|
|
815.5 |
|
|
Solutions to | x | = α
|
|
815.7 |
|
|
Modulus equations
|
|
815.9 |
|
|
Graph sketching when solving modulus equations
|
|
815.9 |
|
|
Modulus equation where there is no solution
|
|
816.1 |
|
|
Biforcation in solution to modulus equation
|
|
816.3 |
|
|
Harder problems requiring forking solutions
|
|
816.7 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Modulus
SLIDE 1
Note – these are duplicates of 00002910001/2.
Consolidation
? What is the difference between distance travelled and displacement?
? Define speed and velocity.
SLIDE 2
? What is the difference between distance travelled and displacement?
Solution
Distance is how far an object travelled in any direction.
Displacement is how far an object is from a point of reference, called the origin.
? Define speed and velocity.
Solution
SLIDE 3
These are displacement-time graphs for four different moving objects, A, B, C and D.
? In each case, find (a) the velocity and (b) the speed of the object.
? There are two pairs of objects with the same speed. Which are they? For each pair, what is their common speed?
SLIDE 4
?
A B
C D
?
SLIDE 5
Modulus
Consider the following statement about a moving object.
The velocity of the object is , but its speed is .
In this statement we are stripping the negative sign from the velocity. In going from velocity to speed we are dropping any negative signs.
Velocity records both (a) the direction in which the object is moving (here positive direction and negative direction relative to a fixed place, called the origin, and (b) the size of the motion. Speed records only the size, or magnitude, of the motion. “How fast it is moving.”
The function that drops the negative signs from objects, and the information about the direction of motion, is called the modulus.
SLIDE 6
Definition of modulus
The symbol . It is called the modulus of x. It is defined by
This means that if x is positive, the modulus of x is positive, but if x is negative, the modulus of x is positive. Stripping a negative symbol from in front of a value, is the same as multiplying that value by .
Piecewise definition
Observe the use of the bracket to give alternative conditions in a definition. If , then , and then .
The two conditions are mutually exclusive, meaning, if you have one, then you cannot have the other. This kind of definition is called piecewise definition, because the function is broken down into a number of pieces.
SLIDE 7
In each case, find the modulus.
? ?
? ?
? ?
SLIDE 8
? ?
? ?
? ?
? ?
? ?
? ?
SLIDE 9
The definition of the modulus is
? What are the functions that correspond to x and in this definition?
? Both of these functions define lines. What are the equations of these lines? What are the gradients and intercepts of these lines?
? Sketch the graph of .
SLIDE 10
This definition may be written
where and .
corresponds to the line with intercept 0 (it passes through the origin), and gradient 1.
corresponds to the line which is the straight line passing through the origin with gradient
SLIDE 11
Sketch the function
SLIDE 12
The graph of is obtained from the graph of by (1) a vertical scaling of 2, followed by (2) a vertical translation of .
SLIDE 13
Sketch the function
SLIDE 14
The graph of is obtained from the graph of by (1) a reflection in the x-axis (a vertical scaling of ), followed by (2) a vertical translation of .
SLIDE 15
Sketch the function
SLIDE 16
The graph of is obtained from the graph of by (1) a horizontal translation by followed by (2) a vertical translation of .
SLIDE 17
Sketch the graph of and find the two solutions to the equation .
SLIDE 18
SLIDE 19
Modulus equations
Example
Solve
Solution
Because this is a linear equation in , we can collect the terms in .
Question
Make a sketch showing the graphs of both and to illustrate the above solution.
SLIDE 20
SLIDE 21
? Solve
? By attempting to solve , explain why this equation has no solution, and make a sketch of and to illustrate this situation.
SLIDE 22
?
?
The modulus can never be less than 0, so this equation has no solution.
The graphs of and have no common point of intersection ? there is no solution to .
SLIDE 23
Example
Solve
Solution
Task
Sketch the graph of to illustrate the above solution
SLIDE 24
To sketch the graph of , we first draw the line and then reflect the negative part in the x-axis.
SLIDE 25
? Solve
? Sketch the graph of to illustrate the solution to .
SLIDE 26
SLIDE 27
? Sketch the graphs of and
? Solve
SLIDE 28
SLIDE 29
? Sketch the graphs of and
? Solve
SLIDE 30
|
|