|
Further elementary vectors |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Harder problems in elementary vectors |
|
Workout |
|
27 slides |
|
| Elementary vectors |
|
Library |
|
12 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTON 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.5] |
 |
|
SOLUTION |
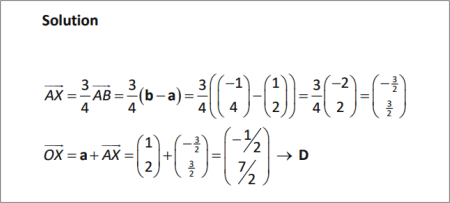 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Consolidation of displacement vectors column form
|
|
824.1 |
|
|
Consolidation of i, j notation
|
|
824.3 |
|
|
Vector division of a line in a ratio
|
|
824.5 |
|
|
Consolidation of working with abstract vectors
|
|
824.9 |
|
|
Vectors in three-dimensions
|
|
825.1 |
|
|
i, j, k notation for three-dimensional vector
|
|
825.1 |
|
|
Colinear is parallel for displacement vectors
|
|
825.3 |
|
|
Recognising parallel / colinear vectors
|
|
825.5 |
|
|
Problems on parallel vectors
|
|
825.7 |
|
|
Uncoupling components of a vector equation
|
|
825.8 |
|
|
Applications of vectors in plane geometry
|
|
825.9 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Further vectors
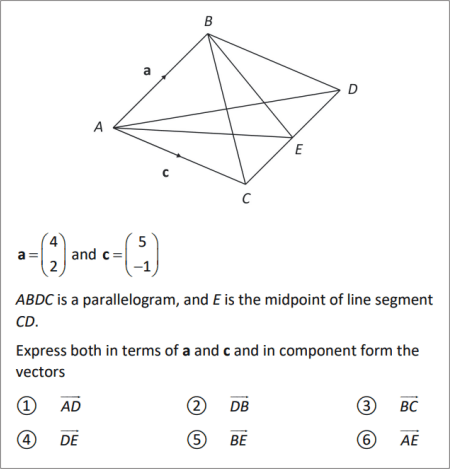
SLIDE 1
and , and E is the midpoint of line segment CD.
Express both in terms of a and c and in component form the vectors
? ? ?
? ? ?
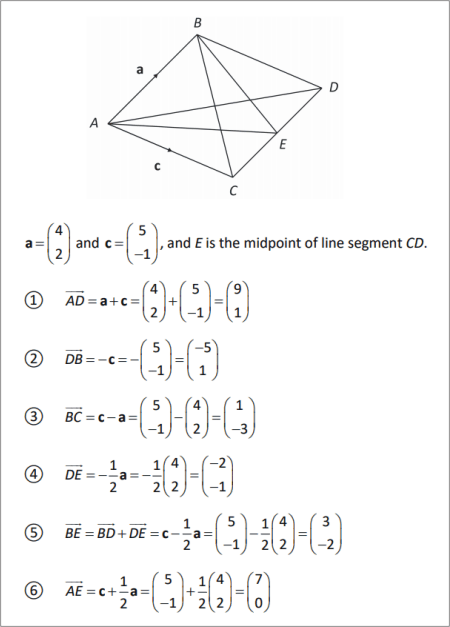
SLIDE 2
and , and E is the midpoint of line segment CD.
?
?
?
?
?
?
SLIDE 3
Evaluate
? ?
SLIDE 4
Evaluate
?
?
SLIDE 5
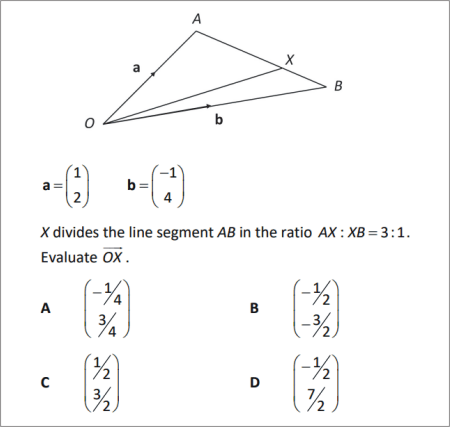
X divides the line segment AB in the ratio . Evaluate .
SLIDE 6
X divides the line segment AB in the ratio .
SLIDE 7
X divides the line segment AB in the ratio .
Evaluate .
SLIDE 8
X divides the line segment AB in the ratio .
SLIDE 9
C is the midpoint of AB. . Find .
SLIDE 10
C is the midpoint of AB. .
SLIDE 11
Vectors in three-dimensions
The triangle ABC has its vertices at the points
.
Find in the form the vectors representing
? ? ?
SLIDE 12
?
?
?
SLIDE 13
In the figure . In plane geometry
? Two line segments are colinear if part of line segment “lies on top of” the other. In the above figure AB is colinear to PQ.
? Two lines are parallel if they are the same distance apart. Alternatively, if they have the same gradient. In the above figure AB is parallel to CD.
Not all parallel lines are colinear. In the above figure, AB is parallel to CD, but not colinear to CD.
? Explain why the distinction between parallel and colinear vectors does not apply. In other words, a colinear vector is also a parallel vector and vice-versa. Hint. All vectors considered here are displacement vectors.
SLIDE 14
Displacement vectors are identical (equal) if they have the same components. In the above figure, although the vectors and are drawn some distance apart, they are in fact the same displacement vector. Hence, we may write .
is longer than , and hence a multiple of . We have
where is a real number. This gives us the criterion for parallel vectors
(Recall that the symbol is called the biconditional and is read, “if, and only if”. It means that each statement implies each other.)
SLIDE 15
Which of the following vectors are parallel to ?
? ?
? ?
?
SLIDE 16
?
?
?
?
?
SLIDE 17
is parallel to the x-axis.
SLIDE 18
Since is parallel to the x-axis,
We uncouple these equations and solve them simultaneously.
SLIDE 19
Applications of vectors in plane geometry
Although any two vectors with the same components are identical, we can use vectors to solve problems in geometry.
Example
The coordinates of the points are and . Show that ACB is a straight line.
Solution
While and could be any parallel vectors in the plane, the geometric problem requires them to the positioned at A. Hence, to prove ACB is a straight line, we only have to show that for some constant .
Hence, A, B and C are colinear and ACB is a straight line.
SLIDE 20
The coordinates of points are and .
? Find
? Show that , where is a constant to be found.
? What can you deduce about the points A, C and B?
SLIDE 21
and .
?
?
? A, C and B are colinear and ACB is a straight line.
Remark
It is not necessary to find to show that the points are colinear. We can find and without reference to the point P.
SLIDE 22
Prove that XYZ is not a straight line.
SLIDE 23
SLIDE 24
OABC is a parallelogram. and . M is the midpoint of CB and N divides AC in the ratio of . Find in terms of x and y and prove that ONM is a straight line.
SLIDE 25
SLIDE 26
M is the midpoint of AB, and CMN is a straight line.
Find the ratio of ON to OA.
SLIDE 27
M is the midpoint of AB, and CMN is a straight line.
To find the ratio of ON to OA.
Solution
|
|