
		blacksacademy.net

Productive and Allocative Efficiency

Productive and allocative efficiency

Productive efficiency is defined to be the production of goods and services at minimum cost. This means that it is not possible to produce more of any one good without producing less of another.

Allocative efficiency, which is also called Pareto efficiency is defined to be a situation where it is not possible to improve one consumer's welfare without making another consumer worse off.

A distribution that is allocatively efficient can be “unfair” in the sense of unequitable. Allocative efficiency is not necessarily a situation in which everyone obtains the same income or an equal distribution of goods.

There is also the concept of technical efficiency. Production is technically efficient when a given quantity of output is produced using the minimum quantity of factor inputs. For example, if a firm could employ fewer workers to produce the same amount of goods, then it is not technically efficient. However, a firm that is technically efficient may not be productively efficient, since there may be some other bundle of the factors of production that might produce the same quantity of goods at a lower cost. For example, a technically efficient firm might employ $1m of capital and 10 workers to produce a given quantity, but by using $2m of capital and 2 workers it might produce the same quantity at lower cost.

Likewise, all allocatively efficient outputs must be productively efficient, but not vice-versa. If a country is not productively efficient then it is possible to increase one consumer's welfare without making another worse off. That is, by becoming productively efficient more goods are produced for no extra factor input. These extra goods can be distributed (allocated), thus making one or more people better off without making anyone else worse off.

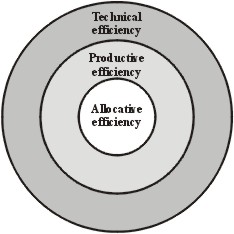
The relationship between the three kinds of efficiency can be represented by the following (Venn) diagram.

The relationship between three kinds of efficiency

Productive efficiency and the allocation of resources

Productive efficiency is concerned with the allocation of resources. At any given time an economy has access to a limited supply of resources. These resources must be distributed to different productive units.

The allocation of resources results in sacrifices. If we spend resources on education rather than defence we forego the benefits of the additional defence. The benefit lost from making one choice rather than another is called by economists its opportunity cost. If you have money to buy just one newspaper, and choose the Financial Times rather than The Telegraph, then the opportunity cost of buying the Financial Times is the benefit that you would have gained from buying The Telegraph.

The idea of opportunity costs is illustrated by means of a production possibility curve. This curve represents the allocation of resources between, for example, two completing goods.

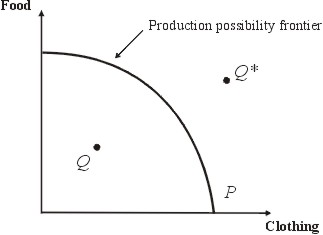
The curve is a “frontier”, showing the most efficient allocation of resources. Along this frontier there is productive efficiency. For example, suppose in a given country only two goods are produced, food and clothing. Then the graph of the production possibility frontier shows the maximum of each good that can be produced using all the resources of the country at maximum efficiency.

Example of a production possibility frontier.

This country produces only food and clothing. Along the frontier there is maximum productive efficiency. Any point within the region, say Q, is a point where the resources are not used efficiently. Any point outside the region, Q*, is a point which is not attainable using the resources of the country within the limitations of the productive techniques available at the time.

The diagram shows that in order to produce more food, some production of clothing must be given up, and vice versa. So this shows that there are opportunity costs involved in making any decision regarding the allocation of resources.

The relationship of productive to allocative efficiency

We have seen that a distribution of goods can only be allocatively efficient if it is productively efficient. We now need to explain why not all productively efficient outputs are allocatively efficient.

Productive efficiency is only concerned with the production of goods. The underlying concept is that of opportunity cost — it examines the opportunity cost of producing more of one good in terms of the lost opportunity of producing another good.

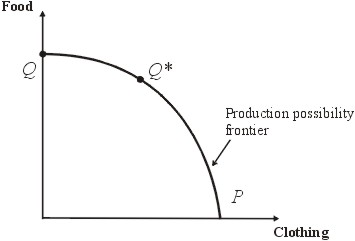
Allocative efficiency is concerned with the value that consumers place on the good. Therefore, it is possible to compare two different productively efficient outputs. The value placed by the consumers on one of these could be greater than the value placed on the consumers. Consider the following situation.

Productive efficiency and value

All points along the frontier are equally productively efficient, but consider the value placed by consumers on the different positions Q and Q*. At Q no clothing is produced. The consumers may enjoy a maximum amount of food, but they will have to walk about naked, as there is no clothing. Unless the climate is warm and constant (for example, in the Garden of Eden) they are not likely to prefer this to a situation such as at Q* where both clothing and food is produced.

Thus, any point on the production possibility boundary is productively efficient, but allocative efficiency is only achieved when the goods and services produced match people's needs and preferences.

Indifference curves

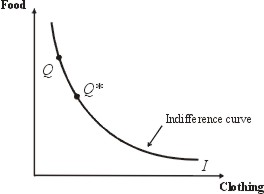
Naturally, economists have a theory to explain these differences of values that consumers place on different combinations (or “bundles”) of goods. Say, for example, one man is choosing between different possible combinations of food and clothing. Suppose 2 units of clothing and 3 units of food gives him the same satisfaction as 1 unit of clothing and 6 units of food (he has less clothing, but is able to eat much more to compensate). In that case the two combinations of food and clothing are said to give him the same level of satisfaction, and he is indifferent to the choice between the two. Combinations of goods that lead to the same level of satisfaction are said to be indifference curves.

An example of an individual indifference curve.

All points lying on the curve yield the same level of satisfaction. At Q more food is consumed than at Q* but at Q* more clothing is consumed than at Q. However, for this individual person, both combinations result in the same level of satisfaction.

If we assume that the more of any good that is consumed the greater the satisfaction, this means that for any individual different satisfaction curves never intersect (they never cross over).

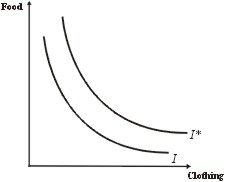
Comparing indifference curves.

All points on I* result in more satisfaction to this particular individual than all points on I. The individual would prefer to consume any combination of goods along I* than any combination on I.

These are just the indifference curves for individuals. However, a community indifference curve can be produced by adding up the indifference curves of individual consumers. The result will be a nest of community indifference curves that will take the same shape as the individual indifference curves.

As all points along the production possibility frontier are productively efficient, and all points along a community indifference curve yield the same satisfaction, allocative efficiency will be achieved at that point on the production possibility frontier that intersects with a community indifference curve yielding the maximum satisfaction.

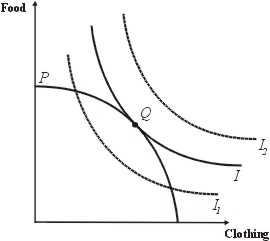
Efficiency and indifference

I is the maximal indifference curve. If we attempt to shift outwards to another indifference curve, say I2, no point on that curve will intersect the production possibility frontier; it is not possible to achieve this level of satisfaction. On the other hand, if we shift inwards to, say I1, then we reduce the total amount of satisfaction that can be achieved, even if we chose a combination of goods that is productively efficient. So there is just one point on the production possibility frontier that is both productively efficient (because it is on the frontier) and allocatively efficient because it lies on an indifference curve that is tangential to the production possibility frontier.

Equity and Pareto efficiency

Equity is concerned with the fairness of the distribution of goods. However, there are different interpretations of what equity or fairness means.

(1)		The individualistic, libertarian approach regards equity has being achieved if everyone has some level of minimum welfare — in terms of income, education, health care and so forth.
(2)		The collectivist or fraternalist apporach — takes the view that everyone should have a distribution of goods that is not far from the average. No one's income should gross exceed that of others.

Pareto efficiency says nothing about the distribution of goods in the sense of equity or fairness. In stepping from an individual indifference curve to a community indifference curve there is a further ingredient required. Suppose a community consists of just two people, A and B. We wish to derive the community indifference curve for them. Suppose we want an indifference curve yielding 10 units of satisfaction along all points. Then we could achieve this indifference curve in an infinite number of ways. For example, we could chose A's indifference curve for 5 units of satisfaction and add it to B's indifference curve for 5 units of satisfaction. But we could just take A's indifference curve of 10 units and ignore B altogether.

In other words, Pareto (or allocative efficiency) says nothing at all about the fairness of the distribution of goods. Distributions of goods resulting in whole sections of the community receiving absolutely nothing could still be allocatively efficient!

Allocative efficiency and the justification of capitalism

In a capitalist society we allow the private ownership of the means of production. Some people have wealth and control capital, and from this they reap profits from production. In such a society there are inequalities of wealth, income and status. Some people would regard this as unfair. Some political theorists attempt to justify the existence of such a system of economic organisation — that is, they attempt to show that the inequalities of wealth and economic power are morally justifiable.

One of the crucial concepts in economic political theory is that of allocative (also called “Pareto”) efficiency. It is argued that, whilst a capitalist system does not lead to equity, more goods are produced than in a command economy, and the result is increased welfare for all. There is some tendency to replace the concept of equity by that of allocative efficiency thus: “A capitalist system may not be equitable but it is allocative efficient”. However, since allocative efficiency is compatible with any kind of distribution of goods, this argument may not be valid!

Utility frontier

In order to illustrate this idea further, Pareto efficiency (allocative efficiency) can be represented by a diagram called a utility frontier.

The diagram shows how the goods produced by the country are distributed. For example, let us assume that there are just two people in the country, A and B. Then along the frontier there is allocative efficiency. What this means that it is not possible to give more to A (for example) without taking away from B.

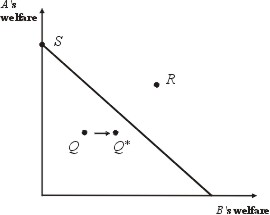
Example of a utility frontier.

Along the frontier it is not possible to make one person better off without making another person worse off. However, within the region bounded by the frontier this is possible. For example, the position Q is not allocatively efficiency, since by shifting to Q* it is possible to give more welfare to B without taking anything away from A. The position R is unattainable since it lies outside the frontier. The diagram illustrates the fact that allocative efficiency says nothing about equity (or “fairness”) — at the position, S, for instance, A receives all the goods, and B gets nothing, but this is still allocatively efficient, since this point lies on the frontier of the utility frontier.

Competition and the efficient allocation of resources

Thus the general claim is that an economic system that is (a) capitalist, meaning permits the private ownership of the means of production, and (b) operates a market economy, meaning allows markets to determine through the price mechanism the quantity produced of each good or service, results in productive and allocative efficiency.

In other words, it is claimed that competition between firms results in increased welfare for all.

To see how this argument might work compare two firms in the same industry, one of which is technically efficient and the other not. Then the company (firm) that is technically inefficient will have lower profits than the one that is. Consequently, in the long run the technically inefficient firm will be driven out of business by the technically efficient firm. Thus, the industry will become technically efficient throughout. Similarly, with productive efficiency. Competition drives out inefficiency.

A similar argument applies to allocative efficiency. Allocative efficiency maximises satisfaction (utility) along the production possibility frontier. This expresses itself in terms of effective demand for goods and services. Therefore, when allocative efficiency is greatest so are profits. Thus a free-market, capitalist system tends to move towards the allocatively efficient point of production.

However, as already indicated, this theory stumbles on the fact that allocative efficiency is completely indifferent to questions of equity and fairness, and yet the challenge to capitalism comes from the desire for an equitable society. Secondly, it shall be shown later that allocative efficiency is only achieved where markets operate according to the model of perfect competition. Since in practice most industries and markets are not perfect, allocative efficiency is not achieved by the capitalist, free-market system. Any existence of market failure, that is, any process that means that a market is unable to achieve allocative efficiency, results in a counterargument against the assumption that competition increases the welfare for all. However, this is a debate in political economics and is worthy of extensive further consideration.