Internal Rate of Return

The internal rate of return is the determination by a graphical method for a given investment of the discount rate which produces a net present value of zero.

This is best illustrated by example.

Example

Calculate the Internal Rate of Return for each of the following three projects. On the basis of these calculations, which project is best?

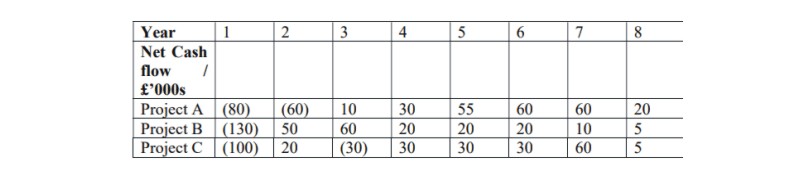
Solution

For each project we need to calculate the Net Present Value at two different discount rates, preferably one that gives a positive value for the Net Present Value, and one that gives a negative value.

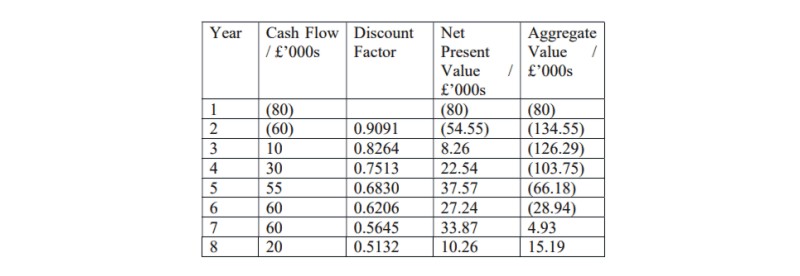
For Project A we will calculate the Net Present Value at discount rates of 10% and at 14%, as follows.

Project A at a discount rate of 10%

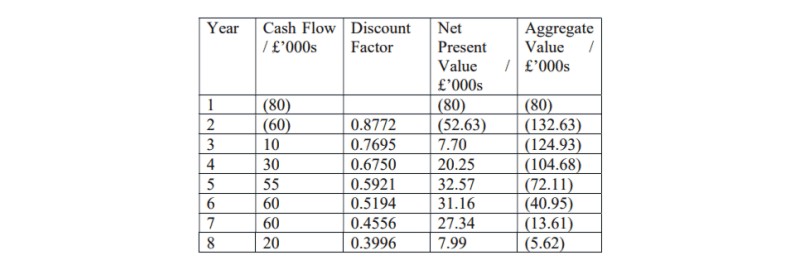
Project A at a discount rate of 14%

This gives us two values of the Net Present Value, at two different discount rates

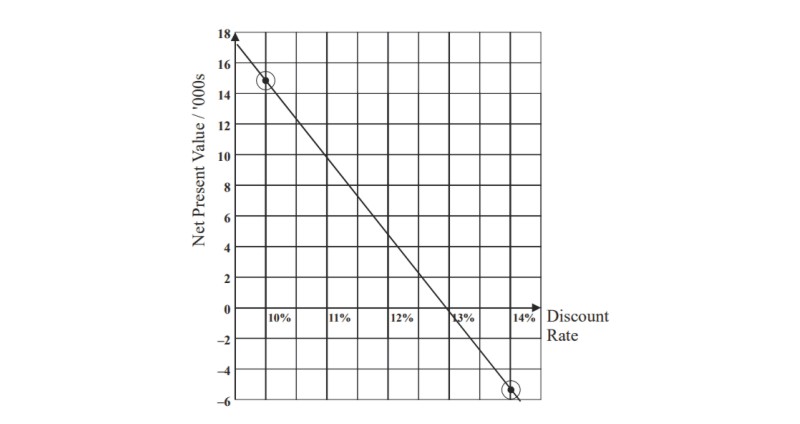
This tells us that the Internal Rate of Return lies between 10% and 14%. To find a more accurate value, we construct a graph of the Rate of Return (horizontal axis) against the Net Present Value (vertical axis). We plot the points

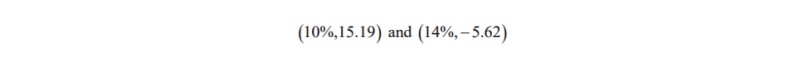
on the graph. We draw the line joining these two points. Then the Internal Rate of Return will be that discount rate that gives a Net Present Value of zero — that is, the point where the line crosses the horizontal axis.

The Internal Rate of Return is 12.9% to the nearest 0.1%.

We now proceed to calculate the discount rate in the same way for the other two investments. We will calculate the net present value of this investment at 12% and 16%.

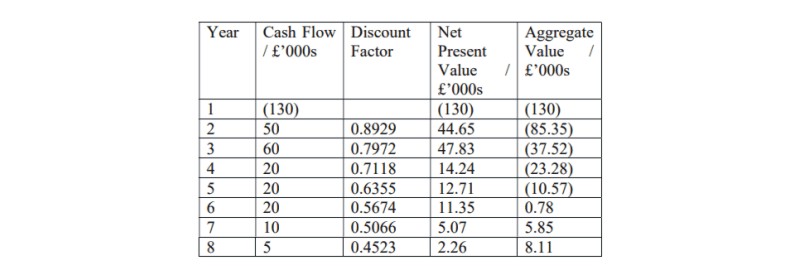
Project B at a discount rate of 12%

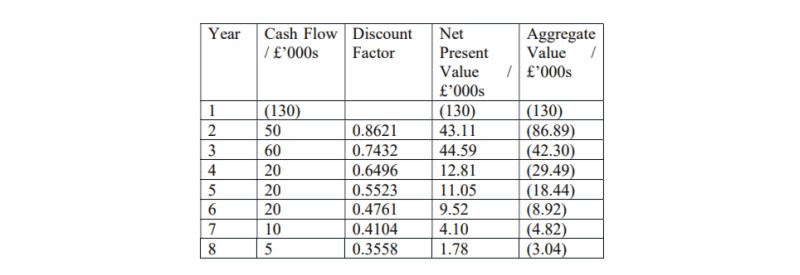
Project B at a discount rate of 16%

At 12% the net present value is £8,110 and at 16% the net present value is a loss of £3,040. So the internal rate of return lies between 12% and 16%.

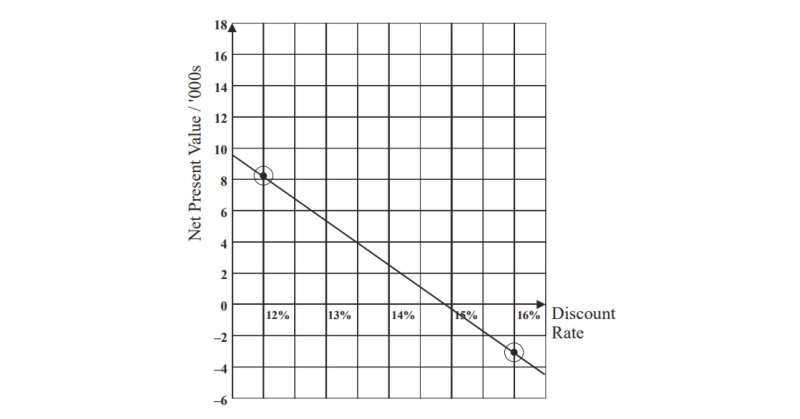
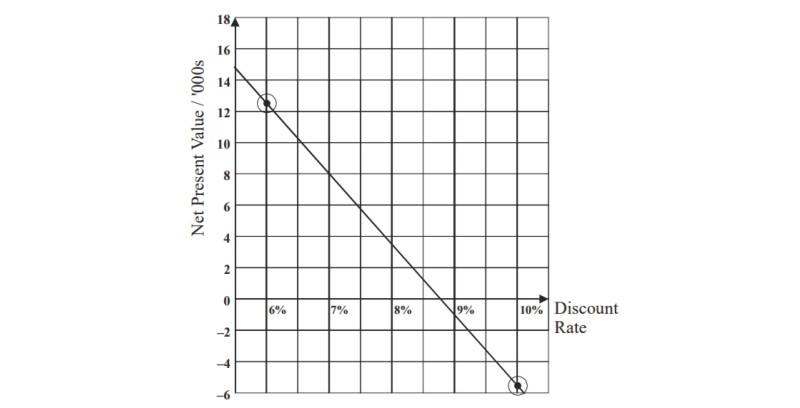
By plotting the points on a graph we can determine a more accurate value for the net present value.

So the Internal Rate of Return is 14.9% to the nearest 0.1%.

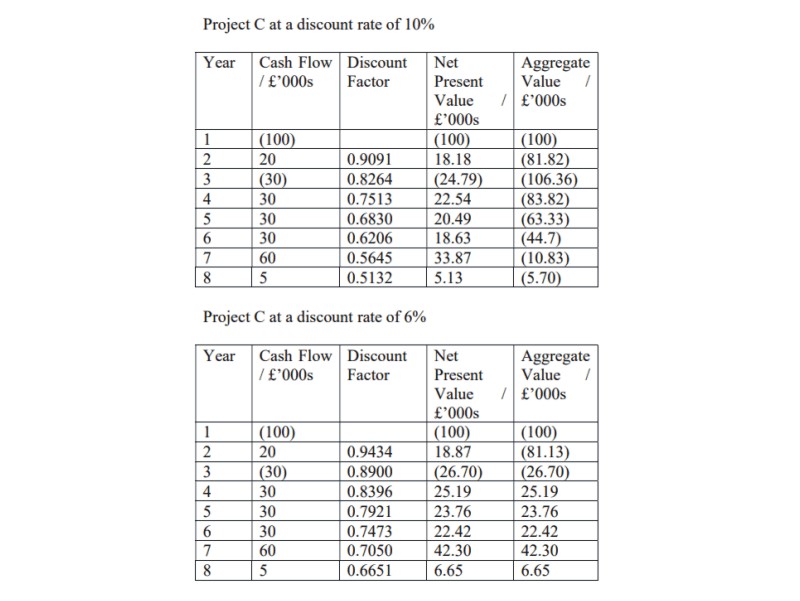
For Project C we will find the net present values at 10% and 6%.

At 6% the net present value is £12,490 and at 10% the net present value is a loss of £5,700. So the internal rate of return lies between 6% and 10%.

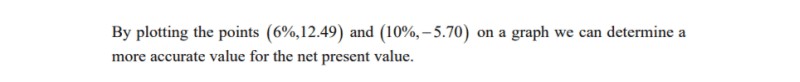
In summary

On the basis of these calculations, the best investment is Project B.