The Paradox of Induction

I. A statement of the paradox

A prescriptive philosophy of science is one that tells us how science ought to work. It tries to define what the correct scientific method will be, and demonstrate that following this procedure will lead necessarily to scientific truth.

One of the reasons why a prescriptive philosophy of science is sought is that there are a number of sceptical problems of a very deep nature which seem to threaten the status of science as knowledge. One of the most profound is the paradox (or problem) of induction. [The term “paradox” is used in an C18th meaning. The C20th meaning of “paradox” implies a formal contradiction. But here the paradox of induction does not involve a contradiction as such — it is rather a “hard problem”]

We attribute to David Hume the first clear exposition of the paradox of induction. He presents it in his Enquiries Concerning Human Understanding. However, a close reading of Hume's text will reveal that he does not intend to pose quite the same problem that it has come to be handed down to us. So, we shall make our first exploration of the paradox in a passage from Bertrand Russell's The Problems of Philosophy.

Now in dealing with this question we must, to begin with, make an important distinction, without which we should soon become involved in hopeless confusions. Experience has shown us that, hitherto, the frequent repetition of some uniform succession or coexistence has been a cause of our expecting the same succession or coexistence on the next occasion. Food that has a certain appearance generally has a certain taste, and it is a severe shock to our expectations when the familiar appearance is found to be associated with an unusual taste. Things which we see become associated, by habit, with certain tactile sensations which we expect if we touch them; one of the horrors of a ghost (in many ghost-stories) is that it fails to give us any sensation of touch. Uneducated people who go abroad for the first time are so surprised as to be incredulous when they find their native language not understood.

And this kind of association is not confined to men; in animals also it is very strong. A horse which has been often driven along a certain road resists the attempt to drive him in a different direction. Domestic animals expect food when they see the person who usually feeds them. We know that all these rather crude expectations of uniformity are liable to be misleading. The man who has fed the chicken every day throughout its life at last wrings its neck instead, showing that more refined views as to the uniformity of nature would have been useful to the chicken.

The paradox of induction is the problem that in all scientific reasoning we form conclusions, called laws, that are of a general nature; however, the evidence we have for those laws is based upon particular experiences. For example, we form the conclusion that all rays of light will be bend as the pass from air into glass, but we have only ever observed a finite number of instances of this law. On further reflection we see that there is no necessary connection between something happening on one occasion and the same thing happening in like circumstances on another occasion. We are not directly acquainted with the “power” behind events that ensures the uniformity of nature throughout space and time.

Another illustration of this might concern the uniformity of space. Imagine that a space mission is about to be sent to the nearest star, Alpha Centuri. People might be queuing up to volunteer to be the first people to witness life on a distant planet. On the other hand, there might be anxious reluctant passengers, desperate not to be dragged on the fool-hardy mission. Why? Because there is no guarantee that the laws of nature operate in the same way in outer space as they do in our solar system. It is entirely conceivable that once the space ship passes beyond the perimeter of our solar system, that entirely different laws of physics will apply, and the space ship could be destroyed by chaotic forces that cannot be anticipated. We have no way at present of being sure that universe is uniform. We have only sampled physical nature in our own limited portion of the universe. We might regard the fear of the passengers as outlandish, but it is not an irrational fear. Just because things have happened at one point of space and at a given time in a certain way is no guarantee that they always will happen that way.

This, then, is the paradox. Every day we reason from particular instances to generalities, and such inference is essential to our way of life; but there is no guarantee that such an inference is valid, and, indeed, very often such inferences prove to be fallacious — as in the case of the chicken that reasoned that its master would always feed it just because its master always has!

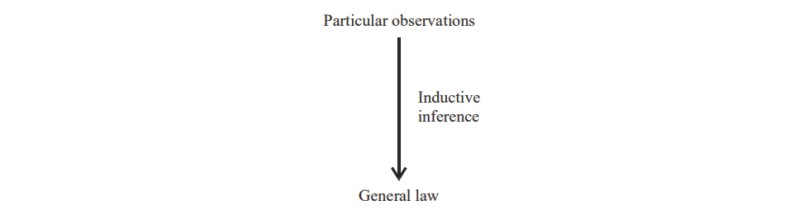
A schematic representation of the inductive inference is as follows.

The paradox of induction

The general law encompasses a potentially infinite number of instances that no amount of observation could possibly affirm. The problem is usually expressed as a problem of inference from past to future, but strictly this is only an instance of the problem; unobserved past events are also subject to the paradox of induction — we can never be sure that any general law has applied uniformly even in the past. No general law can ever be certain.

Yet inductive reasoning is (in the very broadest sense) the basis of science, which constructs laws governing all events. [We have to put this qualifying remark in because science in practice hardly ever employs direct inductive arguments. It proceeds by forming hypotheses and testing these. Nonetheless, the evidence for any scientific theory is based on particular experimental observation, so in the broadest sense science employs induction from particular to general laws. The question of how science actually operates is considered under the heading of the methodology of science. Philosophers of science generally agree that the actual practice of science does not follow an inductive pattern. Yet, the paradox of induction remains. Even so, this point is complicated by the fact that eminent philosophers, such as Karl Popper, have maintained that they have solved the paradox of induction by demonstrating that science does not employ induction. This is considered elsewhere..] One of the purposes of science is to make predictions — in other words to predict that past generalities will also apply in the future.

That this species of reasoning from the particular to the general is unsound is illustrated by the existence of many counter-examples. [Recall that an unsound inference is one where the premises are true but the conclusion is possibly false. In other words, it is possible to construct a possible world in which both the premises and the negation of the conclusion are true. A sound inference is one where, if the premises are true, then the conclusion could not possibly be false..]Russell in his passage gives a number of examples of the way in which inductive reasoning can lead to erroneous conclusions. He points out that if the chicken reasoned that it would always be fed by its owner because it always has been fed by its owner, then it is making an error.

Yet in the formal sense, there is no difference between the reasoning in the chicken's case and the reasoning in science generally. The chicken reasoned, this has always happened in the past, therefore, it always will happen in the future, and that is also how we reason. So the sceptical problem is, what exactly is it that makes scientific generalisations justified?

II. The distinction between Hume's formulation of the problem and the modern version of it

Let us digress briefly to consider the difference between Hume's formulation of the paradox of induction and the formulation in the modern context, as illustrated by the passage from Russell.

Hume did not believe that any knowledge of a cognitive or conscious kind was strictly possible. He maintained that we are forced by the mechanical nature of our minds to believe certain things. We are conditioned by our environment and the structure of our minds to believe that nature is uniform.

The difficulty is that many modern philosophers are not content with this solution to the problem. They wish to demonstrate that science is cognitive knowledge, and that the laws of nature are not just beliefs that are conditioned into us, but true descriptions of a uniform nature arrived at through sound processes of reasoning. The paradox in the modern context is the problem that such processes of reasoning appear to be fundamentally unsound.

Hume's answer is a potential solution to the paradox of induction. It solves the problem by dissolving it — he says that instinctively we must reason inductively, and since we are forced to expect the uniformity of nature from past uniformities, there is little point attempting to justify it.

This answer of Hume's is reflected in Russell's introduction to the paradox which we have just seen, when he writes

Experience has shown us that, hitherto, the frequent repetition of some uniform succession or coexistence has been a cause of our expecting the same succession or coexistence on the next occasion.

Russell acknowledges that past uniformities may cause us to expect future uniformities, but he wants to demonstrate that past uniformities prove that the future will be uniform, and that is his problem. Thus, it is seems that many philosophers wish to maintain that science is true, justified knowledge, and hence they find the paradox of induction disturbing.

It is also worth remarking that Hume, in proposing the paradox of induction, was not intending to cause problems for science. He was endeavouring to undermine the rationalism of Descartes. Descartes claimed that he could derive the whole body of current physics from the existence of God by reason alone. In other words, according to Descartes, science does not require any experiment whatsoever. Hume is (correctly) demonstrating that knowledge of scientific generalisations derives from observation and not from reason. [It is, however, possible to maintain that science derives its truth from both observation (experience) and reason. This is the position adopted by Kant..]

III. Attempts to solve the paradox of induction

There would appear to be no possibility of solving the paradox of induction by justifying induction by deductive reasoning. Inductive reasoning is not a kind of deductive reasoning. There is no reputable Western philosopher who attempts to do this. Furthermore, the problem with inductive reasoning is that it is unsound. The case of the chicken illustrates this. The chicken was wrong to believe it always would be fed because it always has been fed. So no deductive argument could demonstrate that induction was sound.

Likewise, any attempt to justify inductive reasoning by appeal to inductive reasoning would be circular. Russell discusses this possibility in his chapter in The Problems of Philosophy about induction.

It has been argued that we have reason to know that the future will resemble the past, because what was the future has constantly become the past, and has always been found to resemble the past, so that we really have experience of the future, namely of times which were formerly future, which we may call past futures. But such an argument really begs the very question at issue. We have experience of past futures, but not of future futures, and the question is: Will future futures resemble past futures? This question is not to be answered by an argument which starts from past futures alone.

It could be argued that such a process attempts to justify particular uses of induction by appeal to a general principle of induction — a rule of all-encompassing generality, such as “the past future has always resembled the past past, therefore, the future will always resemble the past.” Yet it is clear that this process of reasoning is strictly circular.

There is another passage from Russell introducing another attempt to “solve” the paradox.

It must be conceded, to begin with, that the fact that two things have been found often together and never apart does not, by itself, suffice to prove demonstratively that they will be found together in the next case we examine. The most we can hope is that the oftener things are found together, the more probable it becomes that they will be found together another time, and that, if they have been found together often enough, the probability will amount almost to certainty. It can never quite reach certainty, because we know that in spite of frequent repetitions there sometimes is a failure at the last, as in the case of the chicken whose neck is wrung. Thus probability is all we ought to seek.

However, the claim that “probability is all we ought to seek” also fails to solve the paradox of induction; it is only another example of the previous attempt to justify induction by induction, and is circular. What makes this not clear at first is the ambiguous use of the term “probable” in the argument. This term has two meanings

(a)		When we say, “There is a 1 in 6 probability that a die throw will be a six”, we are giving an example of a scientific general law. The only way to establish this is by throwing the die a very large number of times and finding the ratio of the number of times 6 comes up to the total number of throws.
(b)		When we say, “The existence of God is probable” we are not expressing a scientific general law. We are using the word “probably” to express a belief in the existence of God, but one that also expresses an element of doubt.

When we say “probability is all we ought to seek” we have to ask, are we using “probable” in sense (a) or sense (b). If it is sense (b) then we are really saying that induction is something we believe in, but is not certain, so we have not even attempted to solve the paradox of induction. If it is sense (a), then we are trying to justify induction by appeal to another inductive generalisation, so such an approach is circular.

Another possibility might be that induction is its own justification. The philosopher Swinburn adopts this approach arguing that inductive reasoning is sui generis, its own kind of reasoning, and that in some cases inductive reasoning can reach a state of “confirmation”. If the particular instances of a general law have been observed for a sufficient number of times, then the general law will be confirmed.

Yet this is not a solution either, for it also acknowledges that the paradox of induction cannot be solved, but claims that a weaker state of “knowledge”, which fall short of infallibility, is acceptable. Such a state is that of having a “confirmed” belief. The problem with this is that the chicken's expectation that it would always be fed would surely be confirmed by this rule, so the appeal to confirmation does not sort out “good” inductions from “bad”.

Another attack on the problem of induction comes from the view that science does not actually operate according to the process of inductive inference. The philosopher Karl Popper argues this in his claim that science proceeds by falsificationism. We would need to examine alternative accounts of the methodology of science in order to be able to respond to this claim in detail. Nonetheless, the prospects for such a “solution” do not appear to be very good. The paradox of induction states a sceptical difficulty inherent in any reasoning from particular observations to general laws. Since all science reasons in this way, whatever the precise methodology of science is, scientific reasoning will always be vulnerable to this species of scepticism.

IV. Extrapolation, interpolation and Occam's Razor

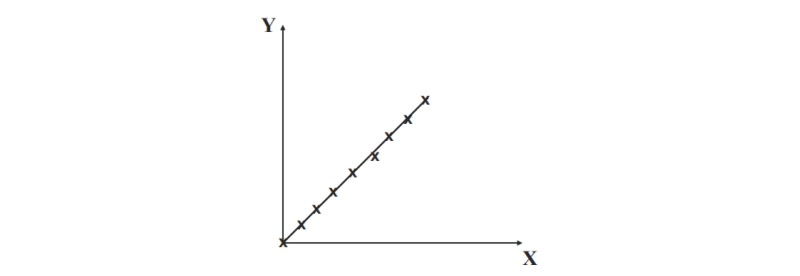
One particular form of the paradox of induction concerns the process in science of analysing results by fitting curves to data points. This results in the extrapolation and interpolation of curves and lines. Extrapolation means to extend a line or pattern beyond the range of the data provided by the experiment. It is illustrated by the following graph.

Proportional relation in empirical science

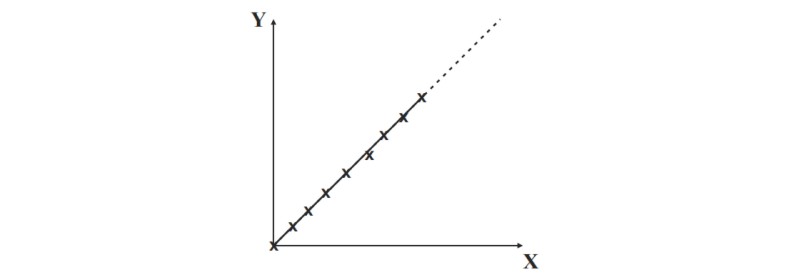
We have a relationship between two variables X and Y and we have plotted a graph of the data, and drawn a straight line. The question is can we now continue the relationship outside the range of values found, and if we do so, should be continue it by means of a straight line? To extrapolate means to carry on a linear relationship outside the given range of values. For example,

Extrapolation

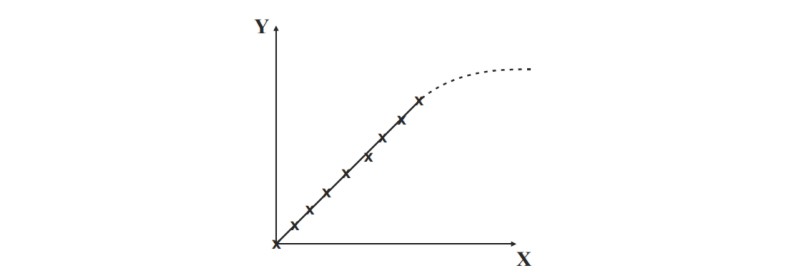
The dotted line represents the extrapolation. However, we do not know for sure that the relationship can be continued in this way; there are any number of alternative possibilities.

Failure of extrapolation

This situation occurs in practical cases all the time. For example, if X was the load on a wire and Y was its extension, then after a point the extension would cease to be proportional to the load and we would see precisely this kind of graph.

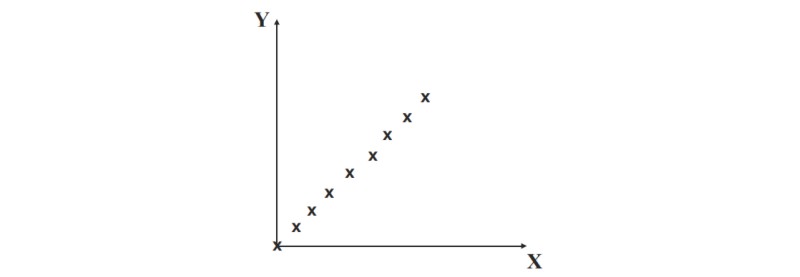
Interpolation is concerned with the problem of fitting a line or relationship between data points. Suppose we start with the following data points.

Empirical observations are discrete and finite

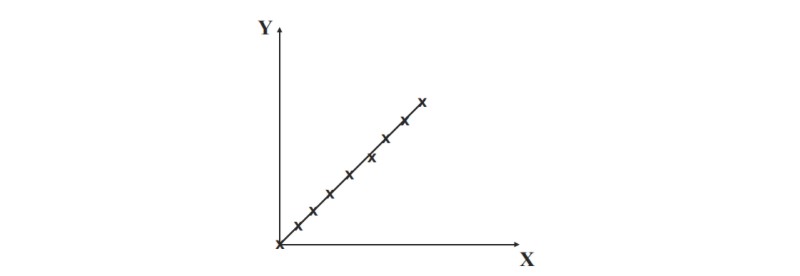
Strictly speaking we have not made observations in the ranges between the data points. We might naturally assume that this was a straight-line relationship, and to fit a straight line to the data is to interpolate between them.

Interpolation of a linear proportional relation into finite data

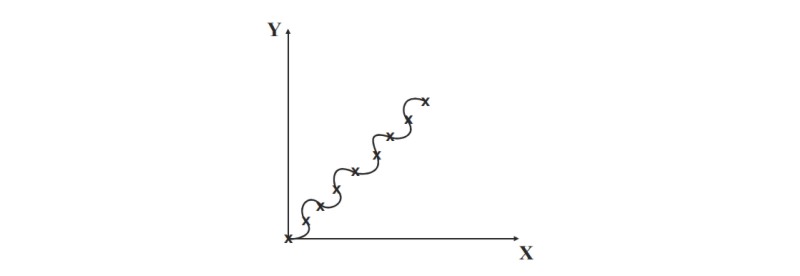
However, there are many other relationships that could be fitted to the same data points.

There is no proof that one interpolation is better than another.

Failure of interpolation

In both cases of extrapolation and interpolation we can see the effect of a psychological law — which is, that when presented with two alternative theories we prefer the simplest. It has been argued that in science we should as a rule prefer the simplest of two competing theories — this rule is called Occam's razor.

Occam's Razor
Given two theories that both explain the evidence equally well, prefer the simplest.

However, this is not a principle that could be used to solve the problem of induction. It would be a scientific general law to say that whenever there are two theories the simplest theory always turns out to be the right one. Such a general law would have to be established by induction, so to use it to justify induction would be circular.

We also have to ask the question: simplest for whom? If we had greater intellectual powers things that we find complex might appear simple to us. Simplicity is relative to our psychological limitations. In applying Occam's razor we are wanting the laws of the universe to be such that we can understand them, but there is no reason offered as to why the universe should be like this.

In short, Occam's Razor cannot be used to solve the paradox of induction.