|
Long multiplication |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Working on long multiplication |
|
Workout |
|
24 slides |
|
| Long multiplication |
|
Library |
|
6 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - CONSOLIDATION 1 |
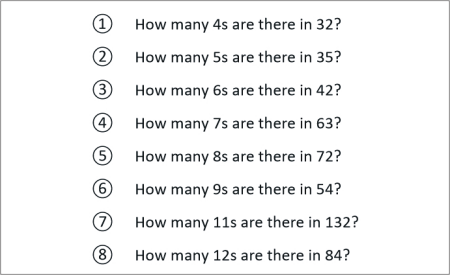 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
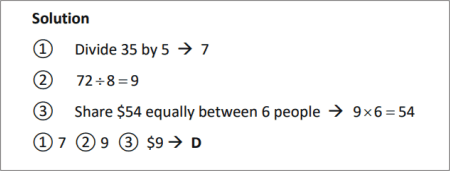 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Sharing and dividing
|
|
378.3 |
|
|
Double digit multiplication as sum of multiples
|
|
378.7 |
|
|
Method: long multiplication
|
|
378.9 |
|
|
Carrying of digit in long multiplication
|
|
379.0 |
|
|
Double digit long multiplication
|
|
379.3 |
|
|
Three digit by two digit long multplication
|
|
379.9 |
|
|
Three digit by three digit long multiplication
|
|
380.3 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Long multiplication
SLIDE 1
? How many 4s are there in 32?
? How many 5s are there in 35?
? How many 6s are there in 42?
? How many 7s are there in 63?
? How many 8s are there in 72?
? How many 9s are there in 54?
? How many 11s are there in 132?
? How many 12s are there in 84?
SLIDE 2
? How many 4s are there in 32? 8
? How many 5s are there in 35? 7
? How many 6s are there in 42? 7
? How many 7s are there in 63? 9
? How many 8s are there in 72? 9
? How many 9s are there in 54? 6
? How many 11s are there in 132? 12
? How many 12s are there in 84? 7
SLIDE 3
? Divide 45 by 5
?
? How many 10s are there in 70?
? Share £48 equally between 6 people
?
?
?
? £126 is shared equally between 11 people and the remainder is given to a charity. How much does the charity get?
SLIDE 4
?
?
? How many 10s are there in 70? Answer 7
? Share £48 equally between 6 people. Each gets £8
?
?
?
? £126 is shared equally between 11 people and the remainder is given to a charity. How much does the charity get?
£5 goes to charity.
SLIDE 3 B
? Divide 45 by 5
?
? How many 10s are there in 70?
? Share $48 equally between 6 people
?
?
?
? 4126 is shared equally between 11 people and the remainder is given to a charity. How much does the charity get?
SLIDE 4 B
?
?
? How many 10s are there in 70? Answer 7
? Share £48 equally between 6 people. Each gets £8
?
?
?
? $126 is shared equally between 11 people and the remainder is given to a charity. How much does the charity get?
$5 goes to charity.
SLIDE 5
? The same number goes into all three boxes. Find the missing number.
? Find the three possible solutions
SLIDE 6
? The same number goes into all three boxes. Find the missing number.
? Find the three possible solutions
SLIDE 7
Example
Complete the following according to the example
?
?
SLIDE 8
?
?
SLIDE 9
?
?
SLIDE 10
Notes for tutors
This complex process must be taught. The diagrams explain how the sum is formed as a summary of the operations on the left.
The placing of the small “2” in “24” must be explained. This small number should not be allowed to be placed anywhere on the page or omitted altogether. It belongs to the “4” in “24” and must be placed near it. The topic of short-term memory is important background educational theory here. Short-term memory refers to the inability to recall on average more than 7 digits after a very short period of seconds. In a complex sum the student cannot remember previous operations. Hence the importance of the “2” as a memory jog.
The placing of the zero representing the tens must be explained.
The systematic multiplication first of and then of must be explained and insisted upon. Badly taught students tend to muddle and mix up these operations. The top row is multiplied systematically by the bottom row. It is usual, but not necessary, to place the larger of the two numbers in the top row. This makes the process easier.
SLIDE 11
Complete the following according to the example
?
?
SLIDE 12
?
?
SLIDE 13
SLIDE 14
SLIDE 15
SLIDE 16
SLIDE 17
SLIDE 18
SLIDE 19
SLIDE 20
SLIDE 21
SLIDE 22
SLIDE 23
SLIDE 24
|
|