|
Beginning probability |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Working on probability |
|
Workout |
|
46 slides |
|
| Beginning probability |
|
Library |
|
18 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Event
|
|
388.1 |
|
|
Certain, uncertain, impossible
|
|
388.1 |
|
|
Counter in box situation
|
|
388.3 |
|
|
More likely, less like, unlikely
|
|
388.5 |
|
|
Even chance
|
|
388.7 |
|
|
Probability
|
|
388.9 |
|
|
Probability NOT (implicit, complement)
|
|
388.9 |
|
|
Probability OR (implicit, disjunction)
|
|
388.9 |
|
|
Probability scale
|
|
389.7 |
|
|
Random event
|
|
389.9 |
|
|
Numerical scale
|
|
389.9 |
|
|
Probability function of event, P(event)
|
|
390.9 |
|
|
Probability in card games
|
|
391.1 |
|
|
Arranging cards by number value
|
|
391.3 |
|
|
Two and three card set
|
|
391.5 |
|
|
Combination (implicit)
|
|
391.7 |
|
|
Four card flush
|
|
392.1 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
PROBABILITY
SLIDE 1
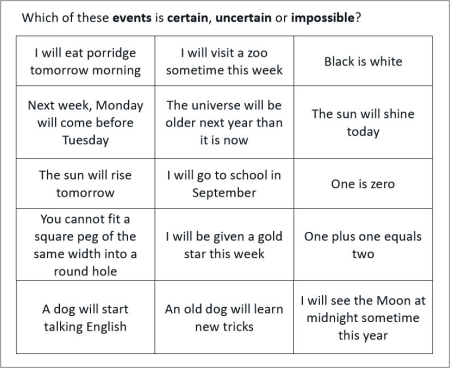
Which of these events is certain, uncertain or impossible?
I will eat porridge tomorrow morning I will visit a zoo sometime this week Black is white
Next week, Monday will come before Tuesday The universe will be older next year than it is now The sun will shine today
The sun will rise tomorrow I will go to school in September One is zero
You cannot fit a square peg of the same width into a round hole I will be given a gold star this week One plus one equals two
A dog will start talking English An old dog will learn new tricks I will see the Moon at midnight sometime this year
SLIDE 2
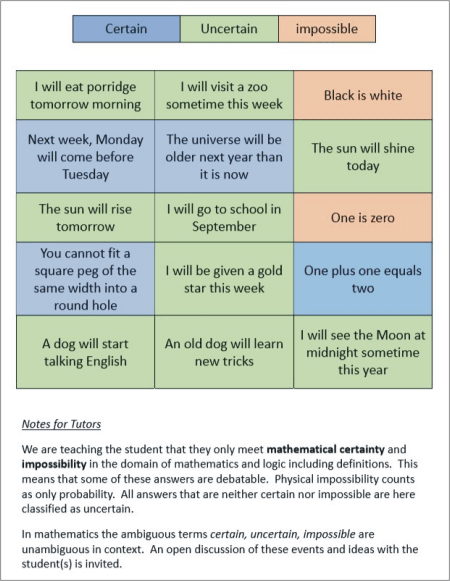
Certain Uncertain impossible
I will eat porridge tomorrow morning I will visit a zoo sometime this week Black is white
Next week, Monday will come before Tuesday The universe will be older next year than it is now The sun will shine today
The sun will rise tomorrow I will go to school in September One is zero
You cannot fit a square peg of the same width into a round hole I will be given a gold star this week One plus one equals two
A dog will start talking English An old dog will learn new tricks I will see the Moon at midnight sometime this year
Notes for Tutors
We are teaching the student that they only meet mathematical certainty and impossibility in the domain of mathematics and logic including definitions. This means that some of these answers are debatable. Physical impossibility counts as only probability. All answers that are neither certain nor impossible are here classified as uncertain.
In mathematics the ambiguous terms certain, uncertain, impossible are unambiguous in context. An open discussion of these events and ideas with the student(s) is invited.
SLIDE 3
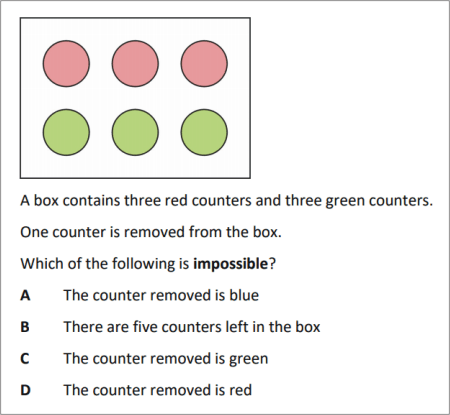
A box contains three red counters and three green counters.
One counter is removed from the box
Which of these statements is certain, uncertain or impossible?
? The counter taken from the box is red
? There will be five counters left in the box
? The counter removed from the box is blue
? The counter removed from the box is green
SLIDE 4
A box contains three red counters and three green counters. One counter is removed from the box
? The counter taken from the box is red ? uncertain
? There will be five counters left in the box ? certain
? The counter removed from the box is blue ? impossible
? The counter removed from the box is green ? uncertain
Notes for tutors
This shows the meaning of the words certain, uncertain and impossible in the mathematical context. All purely physical events (such as “The sun will rise tomorrow”) are classified as uncertain.
SLIDE 5
A box contains one red counter and five green counters.
One counter is removed from the box
Which of these statements is true and certain, false, more likely, unlikely or false and impossible?
? The counter taken from the box is red
? There are five counters left in the box
? There are no counters left in the box
? The counter removed from the box is green
? If another counter is removed, it must be green
? If the counter removed is red, then all the counters left in the box are green.
? The counter removed from the box is not blue
SLIDE 6
A box contains one red counter and five green counters. One counter is removed from the box
? The counter taken from the box is red ? unlikely
? There are five counters left in the box ? true and certain
? There are no counters left in the box ? false and impossible
? The counter removed from the box is green ? more likely
? If another counter is removed, it must be green ? false
? If the counter removed is red, then all the counters left in the box are green ? true and certain
? The counter removed from the box is not blue ? true and certain
SLIDE 7
A game is played in which one counter is removed from a box. There are three versions of this game.
Game 1 Game 2 Game 3
The game is won if a blue counter is drawn.
? In which game is it least likely to win?
? Is there a game which is impossible to win?
? In which game is there an even chance of winning?
? Is there a game where it is certain to win?
SLIDE 8
A game is played in which one counter is removed from a box. There are three versions of this game.
Game 1 Game 2 Game 3
The game is won if a blue counter is drawn.
? In Game 2 it is least likely to win.
? There is no game which is impossible to win, because there is at least one blue counter in each box.
? In Game 1 there an even chance of winning.
? In Game 3 it is certain to win, because all the counters are blue.
SLIDE 9
A box contains one green, one yellow and two blue counters.
A game is played in which one counter is removed from this box.
The probability that the counter is green is
? What is the probability that the counter taken from the box is yellow?
? What is the probability that the counter taken from the box is blue?
? What is the probability that the counter taken from the box is white?
? What is the probability that the counter taken from the box is not green?
? What is the probability that the counter taken from the box is either blue or yellow?
? What is the probability that the counter taken from the box is green, yellow or blue?
SLIDE 10
A box contains one green, one yellow and two blue counters.
A game is played in which one counter is removed from this box.
? The probability that the counter is yellow is
? The probability that the counter is blue is
? The probability that the counter taken is white is 0
? The probability that the counter taken is not green is
? The probability that the counter taken is either blue or yellow is
? The probability that the counter taken is green, yellow or blue is 1.
SLIDE 11
A box contains one green, one blue and one red counter.
A game is played in which one counter is taken from the box.
? What is the probability that the counter is green?
? What is the probability that the counter is black?
? What is the probability that the counter is either green or blue?
? What is the probability that the counter is not green?
? What is the probability that the counter is green, blue or red?
SLIDE 12
A box contains one green, one blue and one red counter.
A game is played in which one counter is taken from the box.
? The probability that the counter is green is
? The probability that the counter is black is 0
? The probability that the counter is either green or blue is
? The probability that the counter is not green is the same as the probability that the counter is blue or red =
? The probability that the counter is green, blue or red = 1
SLIDE 13
?
Probability black = ……
Probability white = …… ?
Probability black = ……
Probability white = ……
?
Probability black = ……
Probability white = …… ?
Probability black = ……
Probability white = ……
SLIDE 14
?
Probability black =
Probability white =
?
Probability black =
Probability white =
?
Probability black =
Probability white =
?
Probability black =
Probability white =
SLIDE 15
Members of a club are voting for a new President. There were four candidates with votes as follows.
Mr. Plum 25
Mr. Green 15
Miss. Scarlet 40
Lord Black 17
One of the ballot papers is opened. Are the following true or false
? In total 95 votes were cast.
? The probability that the paper shows a vote for Mr. Plum is .
? The paper is most likely to show a vote for Miss. Scarlet.
? The paper is least likely to show a vote for Lord Black.
? The probability that the paper shows a vote for Mr. Plum or Mr. Green is the same as the probability that the paper showed a vote for Miss. Scarlet.
SLIDE 16
Members of a club are voting for a new President. There were four candidates with votes as follows.
Mr. Plum 25
Mr. Green 15
Miss. Scarlet 40
Lord Black 17
One of the ballot papers is opened. Are the following true or false
? In total 95 votes were cast. FALSE. 97 votes were cast.
? The probability that the paper shows a vote for Mr. Plum is .
TRUE.
? The paper is most likely to show a vote for Miss. Scarlet. TRUE.
? The paper is least likely to show a vote for Lord Black. FALSE. The least number of votes was cast for Mr. Green.
? The probability that the paper shows a vote for Mr. Plum or Mr. Green is the same as the probability that the paper showed a vote for Miss. Scarlet. TRUE. The combined probability is the same as the probability for Miss. Scarlet, both .
SLIDE 17
Probability scale
One counter is picked at random. Add the following labels to the probability scale.
Less likely More likely
SLIDE 18
SLIDE 19
A sweet-toothed girl had three sweets. Two were chocolate mints and one was a pear drop.
She picked one of these sweets at random.
Label the probability scale matching each of the following to their numerical probabilities.
SLIDE 20
A sweet-toothed girl had three sweets. Two were chocolate mints and one was a pear drop. She picked one of these sweets at random.
SLIDE 21
One counter is taken from the above box.
Mark the probability scale with their values and also with the following labels.
more likely less likely Impossible
SLIDE 22
SLIDE 23
These letters are in a bag
One letter is taken out of the bag at random.
?
?
?
?
SLIDE 24
These letters are in a bag
One letter is taken out of the bag at random.
?
?
?
?
SLIDE 25
One letter is taken at random
?
?
?
?
SLIDE 26
?
?
?
?
SLIDE 27
A six-sided dice has six faces. Map each symbol to a number.
SLIDE 28
SLIDE 29
A six-sided dice is rolled once. Each face is equally likely to come up.
Find
?
?
?
?
?
?
SLIDE 30
A six-sided dice is rolled once. Each face is equally likely to come up.
?
?
?
?
?
?
SLIDE 31
There are four suits in a pack of cards
Clubs Diamonds Hearts Spades
There are thirteen cards in each suit. The last three cards are Jack, Queen and King.
? How many cards altogether are there in a pack of cards?
? One card is taken from a well-shuffled pack of cards. What is the probability that it is the Queen of Hearts?
? One card is taken from a well-shuffled pack of cards. What is the probability that it is a ten?
SLIDE 32
? There are cards in a pack of cards.
? One card is taken from a well-shuffled pack of cards. What is the probability that it is the Queen of Hearts?
? One card is taken from a well-shuffled pack of cards. What is the probability that it is a ten?
SLIDE 33
A set is three cards of the same number
You have been dealt the above hand.
? Arrange the hand so that any two similar numbers are together at the beginning and all the other cards are in ascending order arranged by suit.
? Assuming every card is equally likely to turn up, what is the probability that the next card you will receive will make a three-card set?
SLIDE 34
?
?
6 cards are in your hand, so cards are remaining.
You need a 10 to complete a set. There are two tens remaining. The probability is .
SLIDE 35
? Arrange the hand so that any two similar numbers are together at the beginning and all the other cards are in ascending order.
The Ace is usually considered as “high” and is placed after any number in an arrangement.
? Assuming every card is equally likely to turn up, what is the probability that the next card you will receive will make a three-card set?
SLIDE 36
7 cards are in your hand, so cards are remaining.
There are two ways in which you can make a three-card set, two 6s or two Kings. There are four of these cards remaining. The probability is .
SLIDE 37
A rival player has placed face-up on the table the following set
You hold in your hand the following cards
You will win if you have a set of higher value than your rival.
? Arrange the hand so that any two similar numbers are together at the beginning and all the other cards are in ascending order.
? Assuming every card is equally likely to turn up, what is the probability that when you are next dealt a card you will win?
SLIDE 38
Rival set
? Your hand
? 8 cards are in your hand, 3 cards are on the table, so cards are remaining.
There are two ways in which you can make a three-card set, two 2s or two Queens. But the set of 2s will not beat your rival’s set. There are two Queens remaining, so the probability is .
SLIDE 39
Your rival has placed on the table face-up the following cards
You hold in your hand the following cards
You will win if you have a set of higher value than your rival.
? Arrange the hand so that any two similar numbers are together at the beginning and all the other cards are in ascending order.
? Assuming every card is equally likely to turn up, what is the probability that when you are next dealt a card you will win?
SLIDE 40
Rival hand
? Your hand
? 5 cards are in your hand, 5 cards are on the table, so cards are remaining.
There are two ways in which you can make a three-card set, two 8s or two Jacks. Both will beat your rival’s hand. But one Jack is already on the table. So, there is one Jack remaining and two 8s; three possibilities in total. The probability is .
SLIDE 41
A four-card flush is any continuous sequence of four cards in one suit.
The Ace may be placed either before a 2 or after a King.
You have been dealt the following hand.
? Arrange the hand so that any sequence of cards in the same suit can be seen.
? What is the probability that when you pick up the next card you will have a flush?
SLIDE 42
?
? There are 6 cards in your hand, so cards are remaining. You can obtain a flush with either the 9 of spades or the King of spades. Probability, .
SLIDE 43
You have been dealt the following hand.
? Arrange the hand so that any sequence of cards so that the possibility of a making a four-card flush or a three-card set can be seen.
? What is the probability that when you pick up the next card you will have either a flush or a set?
SLIDE 44
?
? There are 7 cards in your hand, so cards are remaining.
You can obtain a flush with either the 6 of hearts or the 10 of Hearts – two cards in all.
You can obtain a set with either the 7 of Diamonds or the 7 Spades or the 10 of Hearts or the 10 of Clubs – four cards in all.
But the 10 of Hearts can be used to make either a flush or a set, so can be counted only once.
So, there are 5 ways in which to obtain a flush or a set.
Probability, .
SLIDE 45
In a game of cards your rival has placed the following cards face-up on the table.
You have the following hand.
You will win if you have a either a higher valued flush or if two flushes have the same value, then your flush is in a higher-valued suit.
The value of the suits goes:
Clubs (lowest), Diamonds, Hearts, Spades (highest)
What is the probability that with the next card you are dealt you will win?
SLIDE 46
Your rival’s flush is
Rearranging the hand to make the sequences apparent.
It is unfortunate that you cannot make a flush in Diamonds, because your rival has the Jack. If you make a flush in Spades with 7 of Spades, then this has lower value than your rival’s flush. The only way you can win is with the Jack of Spades. There are 4 cards on the table and 6 cards in your hand, making 10 cards in all, so cards remaining. With only 1 possibility of winning, probability .
ERROR IN ANOTHER PREVIOUS QUESTION
155 – 57
?
?
Multiply 6 and 8. Subtract 3. Then divide by 5.
?
|
|