|
Operations |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| One thing at a time |
|
Workout |
|
30 slides |
|
| Operations |
|
Library |
|
11 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
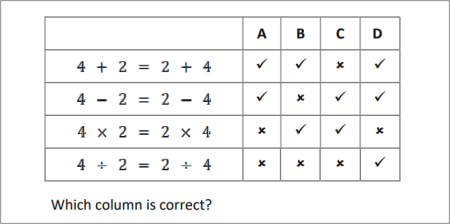
QUESTION [difficulty 0.3] |
 |
|
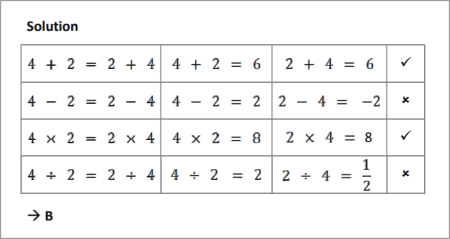
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Operations, +, -, x, Ă·
|
|
422.3 |
|
|
Squence of operations, BODMAS
|
|
423.1 |
|
|
Commutatitivity (implicit)
|
|
423.2 |
|
|
Convention adjacent brackets = product
|
|
423.5 |
|
|
Necessary, unnecessary brackets
|
|
423.9 |
|
|
Use of brackets for clarity
|
|
424.1 |
|
|
Properties of 0
|
|
424.3 |
|
|
Properties of 1
|
|
424.3 |
|
|
Hidden zero
|
|
424.5 |
|
|
Calculator
|
|
424.7 |
|
|
Calculator: use of brackets in denominator
|
|
424.8 |
|
|
Keying sequence
|
|
424.8 |
|
|
By hand
|
|
424.9 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
Which of the following are correct? Put a ? next to those that are correct, and a ? next to those that are wrong.
SLIDE 2
?
?
8
?
?
SLIDE 3
Examples
Use the operations
to make the following equations true
?
?
?
?
?
?
SLIDE 4
?
?
?
?
?
?
SLIDE 5
?
Is this statement true?
?
Is this true or false?
? What is the problem with this argument?
? How can we prevent from being the conclusion of the argument?
SLIDE 6
?
This statement is true because
?
This statement is false.
We can never have in mathematics a statement where two different numbers are equal.
? What is the problem with this argument?
is true
is false
? This is how we went from a true statement to a false statement and how to prevent from being this argument
When we went from the first line to the second line we cancelled out
We are never allowed to cancel out zero
This is also the same as we can never divide by zero
SLIDE 7
? First work out and then multiply by 3
? First work out and then add 9
? Are the two answers the same? Could there be a problem?
? How can we prevent this problem?
SLIDE 8
? =13
?
? 39 is not the same as 21. The two answers are different.
This is a problem, because in mathematics when we use the equal sign, we can never have something like .
? We must make a rule that when we see it must be worked out in only one way.
SLIDE 9
Calculations are worked from left to right with the rule that anything in a bracket is worked out first.
Example
Questions
Work out each of the following in the two different ways indicated by the brackets.
?
?
?
?
SLIDE 10
?
?
?
?
SLIDE 11
Mathematicians have decided on a rule to make it unnecessary to use brackets in some cases.
Multiplication and division always done first unless there is a bracket to say otherwise.
There are other rules, and together these are called the sequence of operations. It is also called BODMAS.
Bracket not needed Bracket needed
This is the same as
Work out
?
?
?
?
SLIDE 12
?
?
?
?
BODMAS
BODMAS is an acronym for brackets, orders, division, multiplication, addition, subtraction.
The notion of an order (power, index, exponent) will be explained in a later chapter.
The order in which addition and subtraction or multiplication and division does not matter. These operations are commutative, meaning that they can be done on their own in any order. The sequence of operations means that multiplication and division (jointly commutative) take precedence over addition and subtraction (jointly commutative).
SLIDE 13
Work out
?
?
?
?
SLIDE 14
?
?
?
?
SLIDE 15
When a number is placed next to a bracket this means multiply.
Examples
Work out
?
?
?
?
SLIDE 16
?
?
?
?
SLIDE 17
?
?
?
?
SLIDE 18
?
?
?
?
SLIDE 19
We sometimes introduce brackets simply in order to make it clear that we are multiplying by a negative number.
Example
The bracket is not needed, and it is often omitted.
Work out
?
?
?
?
SLIDE 20
?
?
?
?
SLIDE 21
?
?
?
?
SLIDE 22
?
?
?
?
SLIDE 23
The numbers 1 and 0 are special numbers. Work out …
?
?
?
?
?
SLIDE 24
?
?
?
?
?
Note
0 is the identity with respect to the operation of addition.
1 is the identity with respect to the operation of multiplication.
SLIDE 25
Which of the following has a hidden zero?
?
?
?
?
SLIDE 26
They all have a hidden zero
?
?
?
?
SLIDE 27
Most calculators work out answers according to the sequence of operations.
This means that if you key into the calculator exactly what you see on the paper, then the calculator will arrive at the correct answer.
The keying sequence for is
5 ( 7 - 3 ) ÷ ( 8 - 6 ) + - 9 =
This will perform all the calculations in the correct order according to the sequence of operations.
What happens to the above calculation if you forget to put the brackets around ?
SLIDE 28
Keying sequence
5 ( 7 - 3 ) ÷ ( 8 - 6 ) + - 9 =
What happens to the above calculation if you forget to put the brackets around ?
You compute
Keying sequence
5 ( 7 - 3 ) ÷ 8 - 6 + - 9 =
You get a totally different answer.
Do not leave a bracket off the bottom of a fraction.
SLIDE 29
Use the calculator to work out
?
?
Work out the answer by hand using the sequence of operations, and compare your results.
SLIDE 30
?
( 9 - 2 ) × ( 7 - 4 ) ÷ ( 1 + 6 ) =
?
( 10 × 4 ) ÷ ( 14 - 9 ) +
( ( 16 + 8 ) ÷ 3 ) =
|
|