|
Patterns and pattern recognition |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
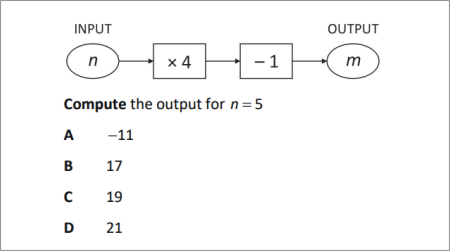
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Number machine
|
|
514.1 |
|
|
Compute
|
|
514.1 |
|
|
Input, output
|
|
514.1 |
|
|
nth term
|
|
514.5 |
|
|
Inverse
|
|
514.7 |
|
|
Multiply out brackets
|
|
514.9 |
|
|
Sequence
|
|
515.1 |
|
|
u(1), u(2), ... u(n) ... notation for terms of a sequence
|
|
515.1 |
|
|
Sequence generated by a rule
|
|
515.3 |
|
|
Linear problems on a sequence
|
|
515.5 |
|
|
Expand and simplify
|
|
515.9 |
|
|
Algebraic problem equating rules
|
|
516.1 |
|
|
Sum successive terms in a sequence
|
|
516.3 |
|
|
Machine flow diagram / chart
|
|
516.5 |
|
|
Trace
|
|
516.5 |
|
|
Pattern rule recognition / problem
|
|
516.7 |
|
|
Pattern investigation
|
|
517.1 |
|
|
Formula for a pattern
|
|
517.3 |
|
|
Conjecture (implicit)
|
|
517.3 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
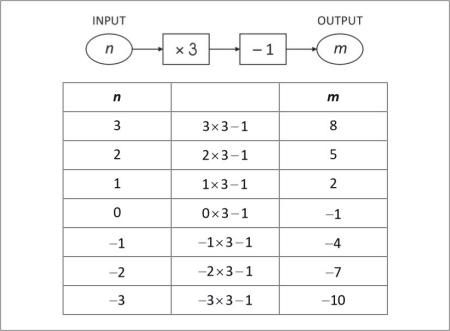
SLIDE 1
Here is a number machine
Compute the output for the following values of n
n m
3
8
2
1
0
SLIDE 2
n m
3
8
2
5
1
2
0
SLIDE 3
Example
Find the equation for each of the following number machines
?
?
?
SLIDE 4
?
?
?
SLIDE 5
A sequence starts
Find its nth term
SLIDE 6
SLIDE 7
Example
The second is called the inverse of the first
Find the inverse
?
?
SLIDE 8
?
?
SLIDE 9
Example
Multiply out the brackets
? ?
? ?
? ?
SLIDE 10
?
?
?
?
?
?
SLIDE 11
A sequence is generated by the following rule
Multiply the previous term by 7 then add 3
The first term is
? Find the second term.
? The sum of the first two terms is 35. Find n.
SLIDE 12
Multiply the previous term by 7 then add 3
The first term is
? Second term ?
?
SLIDE 13
A sequence is generated by the following rule
Multiply the previous term by 3 then subtract 2
The first term is
? Find the second and third terms.
? The sum of the first three terms is 49. Find n.
SLIDE 14
Multiply the previous term by 3 then subtract 2
The first term is
? Second term ?
Third term ?
?
SLIDE 15
A sequence is generated by the following rule
Multiply the previous term by 2 then add 5
The second term of this sequence is
The sum of the first three terms is 55
Find the value of n
SLIDE 16
Second term ?
Since the rule is: multiply the previous term by 2 then add 5
First term ?
Third term ?
Sum ?
SLIDE 17
A sequence is generated by the following rule
Multiply the previous term by 3 then subtract 1
The second term of this sequence is
The sum of the first three terms is 60
Find the value of n
SLIDE 18
Second term ?
Work backwards ? add 1 and divide by 3
First term ?
Working forwards
Third term ?
Sum ?
SLIDE 19
Expand and simplify
Expand and simplify
?
?
?
?
SLIDE 20
?
?
?
?
SLIDE 21
When the two inputs are equal, show that the difference between the outputs is always 14
SLIDE 22
When the two inputs are equal, show that the difference between the outputs is always 14
Solution
Machine OUTPUT
1
2
The difference is
Note: If we subtract y from z we obtain but the difference is 14, because the difference is the bigger less the smaller and is always positive.
SLIDE 23
A sequence is generated by the following rule
Multiply by 2
Complete the following table
Term Value Sum Total
1
2
3
4
5
6
What is the term whose total is ?
SLIDE 24
A sequence is generated by the following rule
Multiply by 2
Term Value Sum Total
1
2
3
4
5
6
The term whose total is is 7. We add one more row.
Term Value Sum Total
7
SLIDE25
Trace each step of this machine when started with ?
What is the print output?
SLIDE 26
Trace
Print output: 18 20 22 24
SLIDE 27
? A pattern has 24 grey squares. What is the number of white squares in this pattern?
? Work out an expression for the difference between the number of grey squares and the number of white squares in the nth pattern.
SLIDE 28
? The number of white squares is two more than half the number of grey squares. For the pattern with 24 grey squares, the number of white squares is 14.
? For the nth pattern
SLIDE 29
? Draw pattern 4
? Work out an expression for the difference between the number of grey squares and the number of white squares in the nth pattern.
SLIDE 30
?
? For the nth pattern
SLIDE 31
Draw all the patterns in the series up to the sixth.
Complete the following table
T
1
1
2
3
3
4
5
6
SLIDE 32
T
1
1
2
3
3
6
4
10
5
15
6
21
SLIDE 33
? Draw similar arrangements for
? Complete the table
T
1
1
1
2
3
3
3
6
4
10
5
15
6
21
? Make a formula for T in terms of n
SLIDE 34
T
1
1
1
2
3
3
3
6
6
4
10
10
5
15
15
6
21
21
SLIDE 35
In this investigation of a geometric pattern, any three horizontal lines may be rotated 90° and vice-versa.
The following diagram shows 2 arrangements of five lines
There are 2 other arrangements of five lines. Find them and draw all 4 possible arrangements of five lines.
SLIDE 36
SLIDE 37
The diagram shows all the arrangements of lines for .
Find all the arrangements of lines for to and complete the following table.
n Arrangements Total
1 1
2
3
4
5 4
6
7
8
SLIDE 38
n Arrangements Total
1 1
2 1
3 2
4 3
5 4
6 6
7 9
8 13
SLIDE 39
For
Complete similar diagrams for
SLIDE 40
SLIDE 41
Use a similar systematic approach to find all the arrangements for
In these exercises, keep a record of your previous results.
SLIDE 42
SLIDE 43
Complete the following table where n is the number of lines and is the corresponding number of arrangements.
n
n
1
7
2
8
3
9
4
10
5
11
6
12
SLIDE 44
n
n
1
7
2
8
3
9
4
10
5
11
6
12
Can you find any relationship or pattern between the numbers?
SLIDE 45
In general, we have
We can prove that this is true for all n.
|
|