|
Lines, regions and inequalities |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - QUESTION 2 |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Coordinate system
|
|
516.1 |
|
|
Point of intersection
|
|
516.2 |
|
|
Equation of line parallel to the y-axis
|
|
516.4 |
|
|
Coordinate distance along a line parallel to axis
|
|
516.4 |
|
|
Integer
|
|
517.0 |
|
|
Inequality
|
|
517.2 |
|
|
Satisfaction / satisfying (a condition)
|
|
517.4 |
|
|
Graph of an inequality - solid line / dashed line
|
|
517.6 |
|
|
Shaded regiion satisfying a system of inequalities
|
|
517.6 |
|
|
Expression where a condition holds
|
|
517.8 |
|
|
Bounded / unbounded region
|
|
518.1 |
|
|
Combining inequalities into one expression
|
|
518.2 |
|
|
Absorbing an inequality
|
|
518.8 |
|
|
Disjunction - either / or
|
|
519.0 |
|
|
Conjunction - and
|
|
519.0 |
|
|
Connected points / region
|
|
519.2 |
|
|
Solid / empty circle diagram for inequalities
|
|
519.5 |
|
|
Symbol for infinity
|
|
519.9 |
|
|
Curly bracket notation for a region
|
|
520.1 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
A coordinate system in two-dimensions has an origin and two axes that are perpendicular to each other. Distances from the origin are marked in the two axes + and - directions.
Onto the above coordinate system plot the points and . Draw the line passing through both these points.
SLIDE 2
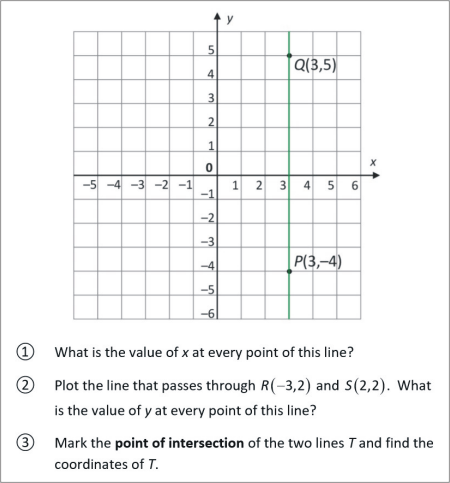
? What is the value of x at every point of this line?
? Plot the line that passes through and . What is the value of y at every point of this line?
? Mark the point of intersection of the two lines T and find the coordinates of T.
SLIDE 3
The value of x at every point of the line PQ is 3.
The value of y at every point of the line RS is 2.
The point of intersection of the two lines is .
SLIDE 4
The line parallel to the y-axis that passes through 3 on the x-axis has equation .
? Draw the line onto the coordinate grid.
? Draw the line onto the coordinate grid.
? Mark the two points of intersection of the parallel with the two perpendicular lines A and B. Find their coordinates and find the distance AB.
SLIDE 5
The distance
SLIDE 6
Plot the lines , , and . Find the points of intersection A, B, C and D. What is the area of the rectangle ABCD?
SLIDE 7
The area of ABCD is
SLIDE 8
Plot the lines , , and . Find the points of intersection A, B, C and D and mark this rectangle ABCD.
Add the lines and to the coordinate grid. Mark the points of intersection of these lines E. Mark F the intersection of lines and . Mark G the intersection of the lines and .
What is the area of the figure ABFEGD?
SLIDE 9
The area of ABFEGD is 34 sq. units
SLIDE 10
An integer is a whole number, positive or negative.
Which of the following are integers?
? 3 ? ? 19.1
? ? 0 ?
SLIDE 11
? 3 is a positive integer
? is a negative integer
? 19.1 is not an integer
? is not an integer
? 0 is an integer
? and is an integer
SLIDE 12
State whether the following are true or false
? ? ?
? ? ?
SLIDE 13
? true
? false
? true
? true
? true
? false
SLIDE 14
? List all the integers satisfying
? List all the integers satisfying and
SLIDE 15
? The integers satisfying are
? The integers satisfying and are 1, 2, 3, 4, 5
SLIDE 16
In a graph an inequality is represented by a dashed line, and an exact inequality by a solid line.
In the above, the shaded region represents the region where and .
State whether the following points are or are not included within this region?
? ? ?
? ? ?
SLIDE 17
? Included, lies within the region
? Included, lies on the boundary of
? Not included, since
? Not included, lies outside the region
? Included,
? Included, . Any point as close as may be to 3 is included.
SLIDE 18
Onto the coordinate grid draw the lines and , and shade the region where both these inequalities hold.
SLIDE 19
Shaded region where and .
SLIDE 20
Onto the coordinate grid draw the lines and .
Shade the region were and , and label it R.
How many points of the type where X and Y are integers lie within this region?
SLIDE 21
R is the region where and . It stretches infinitely off the edges of the visible coordinate grid. We say that the region is unbounded. Because it is unbounded, there are infinitely many points of the type where X and Y are integers that lie within this region. For example, and both lie within this region.
SLIDE 22
Two inequalities and may sometimes be combined into one statement .
Combine the following into one statement
?
?
SLIDE 23
? ?
? ?
SLIDE 24
The coordinate grid has been divided into 9 regions by four lines. Find the inequalities corresponding to each region and state whether the region is bounded or unbounded.
SLIDE 25
Region Definition Bounded/unbounded
?
unbounded
?
unbounded
?
unbounded
?
unbounded
?
bounded
?
unbounded
?
unbounded
?
unbounded
?
unbounded
SLIDE 26
Shade on the coordinate grid the region R defined by
What is the area of this region?
SLIDE 27
R is
The area of the region is 12 sq. units
SLIDE 28
One equality may be absorbed by another
Simplify the following
?
?
?
SLIDE 29
? ?
? ?
? ?
SLIDE 30
When two inequalities are placed side by side, this means either the one or the other.
? Either
It is usual to separate statement meaning either/or with a comma, but this is not necessary.
?
If there is no word between the two statements, the statement means or.
? Either
If we wish to have both statements true simultaneously, then we must use the word and, or an equivalent combination.
?
Sketch on a coordinate grid the region corresponding to
SLIDE 31
SLIDE 32
The shaded region R is defined by the inequalities
A region is connected if any two separate points may be joined by a path passing within the region. In the above, A and B are connected points. C and D are also connected points. But B and C are not connected.
The shaded region R is not connected because the two parts are not connected.
SLIDE 33
Shade onto the coordinate grid the region R corresponding to
State whether the following points are connected within R?
? ?
? ?
SLIDE 34
? connected
? not connected
? not connected
? connected
SLIDE 35
An inequality may be represented by a diagram
A point that is in a set or region is shown with a filled circle
A point that is not in a set or region is shown with an empty circle
Draw diagrams for the following
?
?
?
SLIDE 36
?
?
?
SLIDE 37
Write each of the following diagrams using inequalities
?
?
?
?
SLIDE 38
?
?
?
?
SLIDE 39
The symbol , which is read infinity, represents an unbounded region
means all numbers greater than or equal to 1
We can also express this by
As there is no greatest number, all numbers are unbounded, so the infinity symbol can never be used with an exact inequality
On a coordinate grid draw the region
and
SLIDE 40
and
SLIDE 41
A region can be connected through a single point
Sketch the following region and state whether it is connected.
Note, here defines a region because x is one coordinate and y is the other and coordinates are take the form . To make it clear that this is a region we put the definition within curly brackets.
The region R is made of two smaller regions. The task is to sketch this region and decided whether or not it is connected.
SLIDE 42
R is not connected. The point lines on the boundary of both smaller parts of R, but is not contained in either.
SLIDE 43
Is the following region connected or not connected?
SLIDE 44
R is connected. The point lies on the boundary of both parts of R and is contained in both parts.
SLIDE 45
Reflect A in ? the line and ? the line
SLIDE 46
|
|