|
More about triangles |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Pythagoras and similar triangles |
|
Workout |
|
53 slides |
|
| Triangles |
|
Library |
|
17 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - EXPLANATION |
 |
|
SLIDE 2 - QUESTION 1 |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
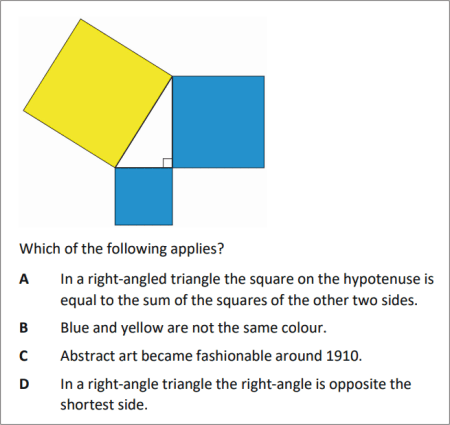 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Hypotenuse
|
|
533.1 |
|
|
Pythagoras's theorem - in words
|
|
533.1 |
|
|
Pythagorean triple
|
|
533.6 |
|
|
Formula for Pythagoras's theorem
|
|
533.8 |
|
|
Construction proving Pythagoras's theorem
|
|
534.0 |
|
|
Similar triangles
|
|
534.7 |
|
|
Ratios in similar triangles
|
|
535.6 |
|
|
Similarity symbol :: = is similar to, is as
|
|
535.6 |
|
|
Overlapping similar triangles
|
|
536.1 |
|
|
Algebraic ratio problem for overlapping similar triangles
|
|
536.2 |
|
|
Finding heights of buildings from similar triangles
|
|
536.6 |
|
|
Distance problem in similar triangles
|
|
536.8 |
|
|
Proof of similarity problem
|
|
537.0 |
|
|
Similar triangles in Pythagoras's theorem
|
|
537.2 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
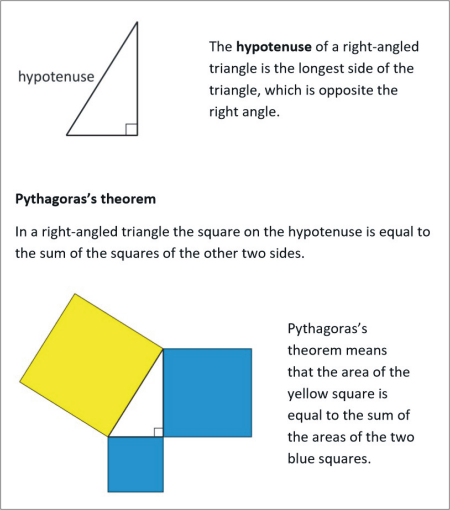
The hypotenuse of a right-angled triangle is the longest side of the triangle, which is opposite the right angle.
Pythagoras’s theorem
In a right-angled triangle the square on the hypotenuse is equal to the sum of the squares of the other two sides.
Pythagoras’s theorem means that the area of the yellow square is equal to the sum of the areas of the two blue squares.
SLIDE 2
Example
In the above diagram, find the length of the hypotenuse, z, to 1 decimal place. You may use a calculator.
Find to 1 d.p. the hypotenuse in the following
? ?
SLIDE 3
? ?
SLIDE 4
? ?
Find y to 1 d.p.
Find x to 1 d.p.
SLIDE 5
?
?
SLIDE 6
The numbers 3, 4 and 5 form a Pythagorean triple
A triangle whose sides are in this ratio is a right-angle triangle
Prove that the following are also Pythagorean triples defining right-angled triangles.
? ? ?
SLIDE 7
?
?
?
SLIDE 8
? Write Pythagoras’s theorem using the symbols a, b and c
? How might the theorem be expressed using the symbols x, y and z, where z represents the hypotenuse?
SLIDE 9
?
?
SLIDE 10
One copy of the pink triangle has been fitted into the yellow square.
Fit another three copies of the pink triangle into the yellow square without overlapping.
SLIDE 11
SLIDE 12
Draw the shape you get if you cut the blue triangle and fit into into ?, and the green triangle and fit it into ?.
SLIDE 13
SLIDE 14
The area of the whole shape is . What is the area of the green square? What is the area of the blue square? How does this prove Pythagoras’s theorem?
SLIDE 15
The area of the green square is . The area of the blue square is . The green and blue squares were obtained from the area of the yellow square by rearrangement. Therefore,
SLIDE 16
Two triangles are similar if all three angles are the same, regardless of the size of the triangles.
Are these two triangles similar triangles?
SLIDE 17
We start by working out the missing angles.
For example,
We see that in both triangles the angles are the same. So, the triangles are similar.
SLIDE 18
Which of the above, if any, are similar?
SLIDE 19
Once we have worked out the missing angles, we see that A and D are similar; and B and C are also similar.
SLIDE 20
When two triangles are similar, the angles that are equal are shown as matching pairs.
SLIDE 21
Use appropriate symbols to identify the angles x and y, and determine which triangles are similar.
SLIDE 22
A and B are similar. C and D are similar.
SLIDE 23
We also use letters and symbols to identify equal angles.
SLIDE 24
By identifying the missing angles in the triangles C, D and F, determine which of these triangles are similar.
SLIDE 25
Similar triangles: A and C, B and F; D and E.
SLIDE 26
When two triangles are similar, their sides are in the same ratio
We say, “4 to 5 to 6 is as 8 to 10 to 12”.
The sides of the second triangle are double those of the first.
The expression is as or is similar to is written with four dots in a square
SLIDE 27
The two triangles are similar.
Express this similarity using the symbol : :
Write this similarity relation also in words.
By how much are the sides of the second triangle bigger than the first?
SLIDE 28
5 to 6 to 8 is as 7.5 to 9 to 12
The sides of the second triangle are 1.5 (one and a half) times the size of the first.
SLIDE 29
Find the lengths x and y
SLIDE 30
The lengths in the second triangle are double those of the first
SLIDE 31
Example
Find x when
Questions
Find x when
? ?
? ?
SLIDE 32
? ?
? ?
SLIDE 33
Find x, giving your answers to 2 decimal places where not exact
? ?
? ?
SLIDE 34
? ?
? ?
SLIDE 35
Find x and y
SLIDE 36
SLIDE 37
Find x and y, giving your answers to 1 dp.
SLIDE 38
We begin by confirming that the two triangles are similar by calculating the missing angles. For example, .
As the two triangles are similar
SLIDE 39
Find x, y and z, giving your answers to 1 dp.
SLIDE 40
We begin by confirming that the two triangles are similar by calculating the missing angles. For example, .
To find x, we use Pythagoras’s theorem
As the two triangles are similar
SLIDE 41 – Similar 13
Overlapping similar triangles
SLIDE 42 – Similar 14
Find x and y
SLIDE 43
SLIDE 44 – similar 15
Find the length BC, giving your answer as a mixed fraction
SLIDE 45
SLIDE 46 – similar 16
A man standing at A can just see the tops of two buildings, B and C, one behind the other. If the man is 2 m tall, find the heights of B and C.
SLIDE 47
SLIDE 46B – similar 16
A man standing at A can just see the tops of two buildings, B and C, one behind the other. If the man is 6 ft tall, find the heights of B and C.
SLIDE 47B
SLIDE 48 – similar 18
Find x
SLIDE 49
Alternatively, the larger triangle is 5 times the smaller.
So,
SLIDE 48B – similar 18
Find x
SLIDE 49B
Alternatively, the larger triangle is 5 times the smaller.
So,
SLIDE 50
Prove that the two triangles are similar and find the heights of the triangles, x and y. Give your answer to 1 decimal place.
SLIDE 51
The angles marked in red are vertically opposite, so equal. The angles marked in green are the base angles of isosceles triangles. Since the angles in red are equal, these must be all equal. So, the two triangles have matching angles and are similar.
To find x we use Pythagoras’s theorem.
Then the triangles are in the same ratio, so
SLIDE 52
Prove that triangle ABC is similar to ADB.
Hint: you must show that they have two equal angles. (If two angles are equal, then the third must be.)
SLIDE 53
Triangles ABC and ADB both have (a) a right-angle, and (b) a common angle A. So, the third angle must be the same, and the two triangles are similar.
By a similar argument, ABC is similar to DBC.
|
|