Investments

sign in || register || pricing

To use the resources of this chapter you must first register

*

ITEM	TYPE	NUMBER
Simple and compound interest	Workout	29 slides
Simple and compound interest	Library	11 questions

Once you have registered, you can work through the slides one by one. The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account. blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.

*

SAMPLE FROM THE WORKOUT

Showing American English version

SLIDE 1 - EXPLANATION

SLIDE 2 - QUESTION 1

*

SAMPLE FROM THE LIBRARY

Showing American English version

QUESTION [difficulty 0.1]

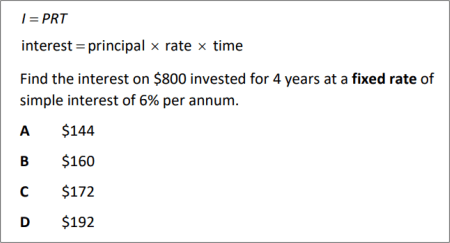SOLUTION

*

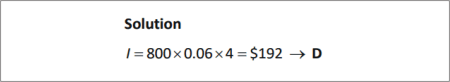DEPENDENCIES

		250: Indices

		254: Investments

		256: Further algebra

*

CONCEPTS

ITEM

LEV.

Simple interest

562.1

Principal (capital investment)

562.1

Method: subtitution and solve problem in simple interest

562.4

Reverse inference in percentage increase / decrease

563.0

Depreciation

563.2

Compound interest

563.4

Evaluation problem for interest

563.7

Exponential growth (implicit)

564.1

Inflation

564.3

Reverse problem finding rate (of interest)

564.5

RAW CONTENT OF THE WORKOUT

To make use of this chapter, please first register. Then you can work through the slides one by one.

What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account.

SLIDE 1 Simple interest Simple interest is the same interest charged at a fixed rate on the original investment. The formula is The word principal is a business term for the sum of money that is invested. The rate is usually given as a percentage but should be converted immediately to a fraction or decimal for the sake of the calculation. The formula, in symbols Example Find the interest on �800 invested for 3 years at 6% per annum SLIDE 2 Find the interest ? on �1500 lent for 5 years at 10% ? on �2000 invested for 7 years at 12% ? on �15,500 invested for 6 years at 3% SLIDE 3 ? �1500 lent for 5 years at 10% ? �2000 invested for 7 years at 12% ? �15,500 invested for 6 years at 3% SLIDE 4 Example If the interest on �800 invested for 3 years is �192, what is the rate of interest? Find the rate of interest for ? �320 to be the interest on �1600 invested for 5 years ? �420 to be the interest on �2000 invested for 3 years ? �264 to be the interest on �600 invested for 4 years SLIDE 5 ? �320 to be the interest on �1600 invested for 5 years ? �420 to be the interest on �2000 invested for 3 years ? �264 to be the interest on �600 invested for 4 years SLIDE 6 Find the length of time for ? �1000 to be the interest on a principal of �5000 invested at 5% per annum ? �480 to be the interest on �3000 invested at 10% ? �1728 to be the interest on �2400 invested at 9% SLIDE 7 ? �1000 to be the interest on a principal of �5000 invested at 5% per annum ? �480 to be the interest on �3000 invested at 10% ? �1728 to be the interest on �2400 invested at 9% SLIDE 8 Find the principal required for the simple interest to be ? �1750 on a principal invested for 5 years at 5% per annum ? �1200 on a principal for 4 years at 6% ? �1700 on a principal for 5 years at 8% SLIDE 9 ? �1750 on a principal invested for 5 years at 5% per annum ? �1200 on a principal for 4 years at 6% ? �1700 on a principal for 5 years at 8% SLIDE 10 Jerry bought a house which he sold to Martha for 20% profit. Martha later sold the house for �324,000 making a loss of 10%. How much did Jerry pay for the house when he first bought it? SLIDE 11 Jerry bought a house which he sold to Martha for 20% profit. Martha later sold the house for �324,000 making a loss of 10%. How much did Jerry pay for the house when he first bought it? Solution Martha sold the house at a 10% loss. Therefore SLIDE 12 A company bought car and used it for three years, after which it was sold to Miki for 40% of the original sale price. This car depreciated over three years by a further 60% from the price for which Miki bought it, when Miki sent it to the breakers, who paid �2,000 for it. What was the original price of the car? To depreciate is to go down in value. SLIDE 13 A company bought car and used it for three years, after which it was sold to Miki for 40% of the original sale price. This car depreciated over three years by a further 60% from the price for which Miki bought it, when Miki sent it to the breakers, who paid �2,000 for it. What was the original price of the car? Solution SLIDE 14 Compound interest In compound interest the interest is added onto (accrues to) the principal (the sum originally invested), and the calculation is begun again on the new sum, and so on. The adding on is called an accrual. Example $1000 is invested at 5% per annum. What is the investment worth at the end of three years? Solution by the �slow� way Solution by the �fast� way SLIDE 15 Find by compound interest ? �250 invested for 2 years at 8% ? �4000 invested for 3 years at 10% ? �1200 invested for 4 years at 6% SLIDE 16 ? �250 invested for 2 years at 8% ? �4000 invested for 3 years at 10% ? �1200 invested for 4 years at 6% SLIDE 17 Ella invests �10,000 for 2 years. She has options from two banks. North Side Bank offers compound interest at 4% per annum. South Side Bank offers 6% for the first year and 2% for the second. Which offer is best? SLIDE 18 Ella invests �10,000 for 2 years. She has options from two banks. North Side Bank offers compound interest at 4% per annum. South Side Bank offers 6% for the first year and 2% for the second. Which offer is best? Solution North Side Bank South Side Bank North Side Bank is better SLIDE 19 Arthur wishes to invest �30,000 for 3 years in a bank. He has two offers. Customer Bank offers 2% for each year. Investment Bank offers 4% for the first year and 1% for the next two years. Which offer is best? SLIDE 20 Arthur wishes to invest �30,000 for 3 years in a bank. He has two offers. Customer Bank offers 2% for each year. Investment Bank offers 4% for the first year and 1% for the next two years. Which offer is best? Solution Customer Bank Investment Bank Customer Bank is better SLIDE 21 At the end of 2010, the population of a town was 5,000. The population increased at the rate of 3% every year. What was the population at the end of 2013? SLIDE 22 At the end of 2010, the population of a town was 5,000. The population increased at the rate of 3% every year. What was the population at the end of 2013? Solution SLIDE 23 Beware of inflation! In 2000 a cookie cost �1. Inflation was at 3% per annum. What did the cookie cost in 2003? SLIDE 24 In 2000 a cookie cost �1. Inflation was at 3% per annum. What did the cookie cost in 2003? Solution SLIDE 25 Blanche invested �1000 for two years at a fixed rate of compound interest. At the end of the two years it was worth $1144.90. Find the rate of interest. Hint. Work by trial and error. Try an interest rate and increase or decrease it until you get a solution. The answer is a whole number rate of interest. Note. There is a more advanced method using logarithms for solving this problem, but it comes later in the development of mathematics. So, here, you are advised to use trial and error. SLIDE 26 Blanche invested �1000 for two years at a fixed rate of compound interest. At the end of the two years it was worth �1144.90. Find the rate of interest. Solution Try 5%. 1000 after 2 years gives 1102.5, too small. Try 6%. 1000 after 2 years gives 1123.6, too small. Try 7%, 1144.90. Answer 7%. SLIDE 27 Depreciation is the reverse of accrual To depreciate means to go down in value. Example A machine that cost �8000 when new depreciates at an annual rate of 25%. Work out the value of the machine after 4 years. Solution SLIDE 28 ? A car was bought new for �22,000. If it depreciates at 20% every year, what is it worth after 8 years? ? A yacht was purchased new for �200,000. It depreciates in value at 10% per annum. What is it worth after 15 years? SLIDE 29 ? A car was bought new for �22,000. If it depreciates at 20% every year, what is it worth after 8 years? ? A yacht was purchased new for �200,000. It depreciates in value at 10% per annum. What is it worth after 15 years?