|
Further algebra |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Further work in algebra |
|
Workout |
|
72 slides |
|
| Further algebra |
|
Library |
|
20 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
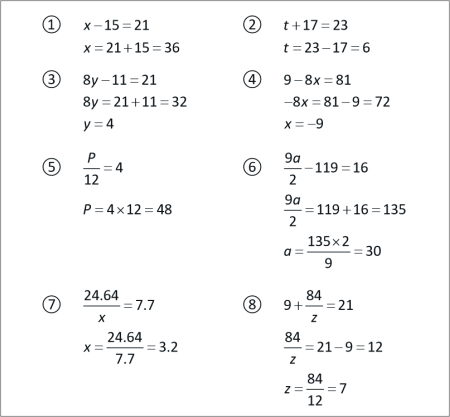 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
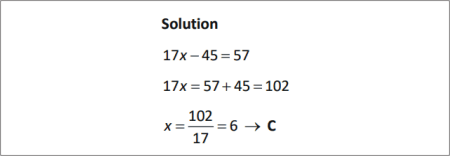 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Consolidation of methods of linear equations
|
|
566.1 |
|
|
Consolidation of problem in an unknown quantity
|
|
566.9 |
|
|
Consolidation of pseudo geometric problem
|
|
567.1 |
|
|
Solution by inspection
|
|
567.3 |
|
|
Box problem
|
|
567.5 |
|
|
Right-triangle problem
|
|
567.7 |
|
|
Expand and solve
|
|
568.1 |
|
|
Algebraic pseudo angle problem
|
|
568.3 |
|
|
Equal perimeter problem
|
|
569.0 |
|
|
Cross-multiplying
|
|
569.1 |
|
|
Numerator and denominator problem
|
|
570.2 |
|
|
Similar triangle cross-ratio problem
|
|
570.4 |
|
|
Function notation
|
|
570.8 |
|
|
Argument and value
|
|
571.1 |
|
|
Formation of a function
|
|
571.5 |
|
|
Equating functions
|
|
571.8 |
|
|
Positive and negative solutions to roots
|
|
572.1 |
|
|
Equating functions problem
|
|
572.5 |
|
|
Factorising
|
|
572.7 |
|
|
Substituting for letters / symbols
|
|
572.9 |
|
|
Two or three step direct substitution problem
|
|
573.1 |
|
|
Ratio proof of Pythagoras's theorem
|
|
573.5 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
Consolidation
Solve
? ?
? ?
? ?
? ?
SLIDE 2
? ?
? ?
? ?
? ?
SLIDE 3
Consolidation
Solve
? ?
Find the positive value such that
? ?
Solve
? ?
SLIDE 4
? ?
? ?
? ?
SLIDE 5
Solve
? ?
SLIDE 6
? ?
SLIDE 7
What is the fundamental rule for equations?
In each of the following the fundamental rule has not been applied and one or more blunders have been made. Explain what the blunders are and give the correct version.
?
?
SLIDE 8
Fundamental rule for equations
What you do to all of one side of the equation you also do to all the other.
?
The blunder is that everything should be multiplied by 6.
Correct
?
The first blunder is that should be subtracted from the left-hand side; the second blunder is that the minus sign in front of 21 has been left out.
Correct
SLIDE 9
Alice is 8 years younger than Beatrice. Candice is twice the age of Beatrice. The sum of all their ages is 40. What are their ages?
SLIDE 10
Alice is 8 years younger than Beatrice. Candice is twice the age of Beatrice. The sum of all their ages is 40. What are their ages?
Solution
Let Beatriceís age be x.
Then, Aliceís age is and Candiceís age is .
The sum of their ages is 40 ?
Alice is 4, Beatrice is 12 and Candice is 24.
SLIDE 11
The diagram shows a rectangle. The area of the rectangle is 475 sq. units. What is the length y of the rectangle?
SLIDE 12
SLIDE 13
Two numbers add to 100. One of the numbers is a square number. The other number is a prime number. What are the two numbers?
SLIDE 14
Two numbers add to 100. One of the numbers is a square number. The other number is a prime number. What are the two numbers?
Solution
This is solved by inspection. We examine all the square numbers and find the difference with 100. The answer will the one whose difference is a prime number.
1 1 99 6 36 64
2 4 96 7 49 51
3 9 91 8 64 36
4 16 84 9 81 19
5 25 75 10 100 0
The square number is and the prime number is 19.
In this solution we could have omitted the even numbers, and note also that 91 is a composite number, .
SLIDE 15
There are two boxes. Box A contains £2.40 in 5p coins, and Box B has only 2p coins in it. The number of coins in Box B is the number of coins in Box A. How much money does Box B contain?
SLIDE 16
There are two boxes. Box A contains £2.40 in 5p coins, and Box B has only 2p coins in it. The number of coins in Box B is the number of coins in Box A. How much money does Box B contain?
Solution
SLIDE 17
Find the length x, giving your answer to 1 decimal place.
SLIDE 18
SLIDE 19
Expanding brackets
Expand
? ?
? ?
SLIDE 20
?
?
?
?
SLIDE 21
Expand and solve
Expand and solve
? ?
? ?
SLIDE 22
?
?
?
?
SLIDE 23
The angles are measured in degrees. Find the angles.
SLIDE 24
SLIDE 25
The area of the square A is 64 cm2. The perimeter of the circle B is equal to the perimeter of A. What is the area of B? Give your answer to 3 significant figures.
SLIDE26
The area of the square A is 64 cm2. The perimeter of the circle B is equal to the perimeter of A. What is the area of B?
Solution
SLIDE 25B
The area of the square A is 64 in2. The perimeter of the circle B is equal to the perimeter of A. What is the area of B? Give your answer to 3 significant figures.
SLIDE26B
The area of the square A is 64 in2. The perimeter of the circle B is equal to the perimeter of A. What is the area of B?
Solution
SLIDE 27
The radius of the circle B is . The perimeter of the rectangle A is equal to the circumference of B. Find the area of B. Give your answer to 3 significant figures.
SLIDE 28
The radius of the circle B is . The perimeter of the rectangle A is equal to the circumference of B. Find the area of B. Give your answer to 3 significant figures.
Solution
SLIDE 29
Cross-multiplying
Example
Cross-multiply and solve
SLIDE 30
Solve
? ?
? ?
SLIDE 31
?
?
?
?
SLIDE 32
When a number is added to both the numerator and denominator of the fraction the result is the new fraction . Find this number.
SLIDE 33
When a number is added to both the numerator and denominator of the fraction the result is the new fraction . Find this number.
Solution
SLIDE 34 Ė The picture is similar 17 from the workout 243
Find the distance x
SLIDE 35
SLIDE 34B Ė The picture is similar 17B from the workout 243
Find the distance x
SLIDE 35B
SLIDE 36
Triangles A and B are similar right-angled triangles. Measurements are in centimetres. Find the area of B, giving your answer to 3 significant figures.
SLIDE 37
Triangles A and B are similar right-angled triangles. Measurements are in centimetres. Find the area of B.
Solution
Substituting gives the hypotenuse of B to be .
By Pythagorasís theorem
SLIDE 36B
Triangles A and B are similar right-angled triangles. Measurements are in inches. Find the area of B, giving your answer to 3 significant figures.
SLIDE 37B
Triangles A and B are similar right-angled triangles. Measurements are in inches. Find the area of B.
Solution
Substituting gives the hypotenuse of B to be .
By Pythagorasís theorem
SLIDE 38
Function notation
The symbol is said, ďf of xĒ
It represents the result of applying a rule to a number.
Example
SLIDE 39
? . Find .
? . Find and .
? . Find when .
? . Find when .
SLIDE 40
?
?
?
?
when
SLIDE 41
x is called the argument of the function f
y is called the value of the function f for the argument x
? . Find the value when the argument is 4.
? . Find the value when the argument is 0.4.
SLIDE 42
?
When the argument is , the value is
?
When the argument is the value is
SLIDE 43
If what is the value of x when ? Give your answer to 3 significant figures.
SLIDE 44
If what is the value of x when ?
Solution
SLIDE 45
Formation of a function
When High Street School was opened in year 0, there were 18 students taking mathematics. Since opening, the number of students taking mathematics has been increasing by 15 students at the beginning of each new academic year. Find the function, , for the number of students n academic years after opening. What was the number of students at the school taking mathematics five years after opening?
Solution
SLIDE 46
In a town the number of pet owners on 1 Jan 2000 was 50. Between 2000 and 2020 the number of pet owners increased by 12 per year by the first day of the next year. Find the function for the number of pet owners on 1 Jan of each year, where n is the number of whole years. What was the number of pet owners in the town on 1 Jan 2012?
SLIDE 47
In a town the number of pet owners on 1 Jan 2000 was 50. Between 2000 and 2020 the number of pet owners increased by 12 per year by the first day of the next year. Find the function for the number of pet owners on 1 Jan of each year, where n is the number of whole years. What was the number of pet owners in the town on 1 Jan 2012?
Solution
SLIDE 48
Equating functions
Find x when
Solution
SLIDE 49
?
?
SLIDE 50
?
?
SLIDE 51
Positive and negative solutions
Find all the solutions, positive and negative. Give your answers to 3 significant figures where the solutions are not exact.
? ?
? ?
? ?
SLIDE 52
?
?
?
?
?
?
SLIDE 53
?
?
SLIDE 54
?
?
SLIDE 55
In 1990 a town had 3000 dogs and 1500 cats. The number of dogs went down by 45 each year, and the number of cats increased by 30 each year. Find the year in which the number of dogs was equal to the number of cats.
SLIDE 56
In 1990 a town had 3000 dogs and 1500 cats. The number of dogs went down by 45 each year, and the number of cats increased by 30 each year. Find the year in which the number of dogs was equal to the number of cats.
Solution
In the year 2010 the dogs were equal to the cats
SLIDE 57
Factorising
Factorise the following
? ?
? ?
SLIDE 58
?
?
?
?
SLIDE 59
Substituting for letters
?
? , giving your answer to 3 significant figures.
SLIDE 60
?
?
SLIDE 61
SLIDE 62
Solution
SLIDE 63
SLIDE 64
Solution
SLIDE 65
State Pythagorasís Theorem
SLIDE 66
Pythagorasís theorem
In a right-angled triangle the square on the hypotenuse is equal to the sum of the squares of the other two sides.
Pythagorasís theorem means that the area of the yellow square is equal to the sum of the areas of the two blue squares.
Using the symbol z for the hypotenuse of a right-angled triangle, and x and y for the other two sides, state an algebraic version of Pythagorasís theorem.
SLIDE 67
Pythagorasís theorem
In a right-angled triangle, where z denotes the hypotenuse
SLIDE 68
Prove that triangle ABC is similar to ADB.
Hint: you must show that the have two equal angles.
(If two angles are equal, then the third must be.)
SLIDE 69
Triangles ABC and ADC both have (a) a right-angle, and (b) a common angle A. So, the third angle must be the same, and the two triangles are similar.
By a similar argument, ABC is similar to DBC.
SLIDE 70
Triangle ABC is similar to ADB and BDC
By finding what are equal to in the triangle ADB, show that .
SLIDE 71
Find , and hence prove Pythagorasís Theorem.
SLIDE 72
Therefore,
|
|