|
Quadrilaterals and polygons |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Further geometry |
|
Workout |
|
34 slides |
|
| Quadrilaterals and polygons |
|
Library |
|
26 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.7] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Consolidation of area formulas
|
|
576.3 |
|
|
Convex and concave polygons
|
|
576.5 |
|
|
Sum of interior angles of a quadrilateral
|
|
576.7 |
|
|
Sum of interior angles of polygons
|
|
577.3 |
|
|
Consolidation interior / exterior angles of polygon
|
|
577.8 |
|
|
Tessellation, tiling
|
|
577.9 |
|
|
Regular quadrilateral = square
|
|
577.9 |
|
|
Regular tessellation
|
|
577.9 |
|
|
Impossibility proof in context of tessellation
|
|
578.0 |
|
|
Regular square, triangular, hexagonal tessellations
|
|
578.1 |
|
|
Semi-regular tessellation
|
|
578.3 |
|
|
Result: mid-point parallelogram
|
|
578.6 |
|
|
Cyclic quadrilateral
|
|
578.9 |
|
|
Tangent to a curve
|
|
579.1 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
Revision
Define the following geometric shapes and explain in words how to find their areas. Explain also what they have in common with each other.
? Parallelogram
? Trapezium
? Rhombus
? Kite
SLIDE 2
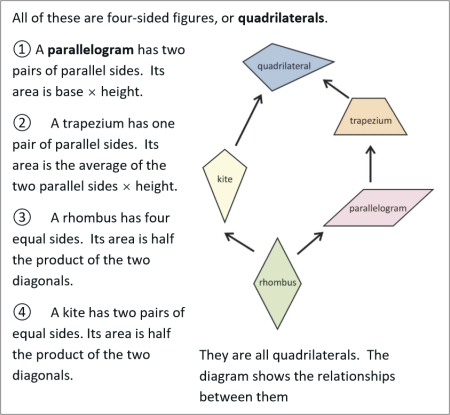
All of these are four-sided figures, or quadrilaterals.
? A parallelogram has two pairs of parallel sides. Its area is base height.
? A trapezium has one pair of parallel sides. Its area is the average of the two parallel sides height.
? A rhombus has four equal sides. Its area is half the product of the two diagonals.
? A kite has two pairs of equal sides. Its area is half the product of the two diagonals.
They are all quadrilaterals. The diagram shows the relationships between them
SLIDE 3
Revision
Write the algebraic formula for the area of each of the following.
? Parallelogram
? Trapezium
? Rhombus
? Kite
SLIDE 4
? Parallelogram
where b is the base and h the height
? Trapezium
where a and b are the lengths of the parallel sides and h is the height (the distance separating the parallel sides).
? Rhombus
where a and b are the lengths of the diagonals.
? Kite
where a and b are the lengths of the diagonals.
SLIDE 5
Convex and concave
In a convex polygon no interior angles are greater than 180°. If any interior angle is greater than 180°, then the polygon is concave.
Give a name to each of the above polygons.
SLIDE 6
? Convex pentagon ? Concave hexagon
? Concave heptagon ? Convex quadrilateral
SLIDE 7
Any quadrilateral can be divided into two triangles.
What is the sum of the interior angles of any quadrilateral?
SLIDE 8
Since the sum of the angles of two triangles is 180°, the sum of the interior angles of any quadrilateral is 360°.
SLIDE 9
Find the angle a
SLIDE 10
SLIDE 11
Find the angle a
SLIDE 12
In the isosceles triangle the base angle is 58°
In the quadrilateral, the angle including a is 110°
So,
SLIDE 13
By dividing each polygon into triangles find the sum of their
interior angles and complete the table.
Number of sides Name Triangles Sum of interior angles
3 Triangle 1 180°
4 Quadrilateral 2 360°
5 Pentagon 3 540°
6
7
8
9
10
n
SLIDE 14
Number of sides Name Triangles Sum of interior angles
3 Triangle 1 180°
4 Quadrilateral 2 360°
5 Pentagon 3 540°
6 Hexagon 4 720°
7 Heptagon 5 900°
8 Octagon 6 1080°
9 Nonagon 7 1260°
10 Decagon 8 1440°
n n-sided polygon
SLIDE 15
In the pentagon angle b is twice the size of angle a.
Find the angles a and b.
SLIDE 16
The interior angle whose exterior angle is 241° is
Since and the sum of the interior angles of a pentagon is 540°
SLIDE 17
A regular polygon is a polygon whose sides are all equal.
A regular polygon can be inscribed within a circle.
Find the interior and exterior angles of a regular pentagon, hexagon and octagon.
SLIDE 18
Sides Name Triangles Sum interior angles Interior
angle Exterior
Angle
5 Pentagon 3 540° 108° 72°
6 Hexagon 4 720° 120° 60°
8 Octagon 6 1080° 135° 45°
SLIDE 19
A tessellation is a covering of a surface that leaves no gaps.
A tessellation is also called a tiling.
The regular quadrilateral is the same as a square.
A regular tessellation is a covering with a regular polygon.
Show that it is not possible to make a regular tessellation with the pentagon.
SLIDE 20
Show that it is not possible to make a regular tessellation with the pentagon.
The interior angle of a pentagon is 108°. If we put two pentagons together, the exterior angle they make is 144°, which cannot be the interior angle or multiple of interior angles of a pentagon.
SLIDE 21
In addition to the square tiling, there are only two other regular tessellations. What are they?
SLIDE 22
Regular triangular tessellation Regular hexagonal tessellation
SLIDE 23
A semi-regular tessellation is a tessellation made of one than one regular polygon in a repeated pattern.
SLIDE 24
A semi-regular polygon is to be made by attaching twelve-sided polygons to squares. Show that the third shape in the pattern is a regular hexagon and draw the tessellation.
SLIDE 25
Since the interior angle of a regular twelve-sided polygon is 150°, and the interior angle of a square is 90°, the interior angle of the third shape is . As it is regular, it must be a hexagon.
SLIDE 26
The mid-point of the line AB in the quadrilateral has been marked. Mark the other mid-points, labelling them N, O and P respectively. What kind of quadrilateral does MNOP look like?
SLIDE 27
It looks like a parallelogram.
Prove that MNOP is a parallelogram.
SLIDE 28
The sides of triangle ABD are twice the size of the sides of triangle AMP, so they are similar triangles. The angles correspond, and MP is parallel to BD.
Likewise, NO is parallel to BD, so MP is parallel to NO since they are both parallel to BD.
Likewise, MN is parallel to OP because they are both parallel to AC.
Hence, MNOP is a parallelogram.
This applies to all quadrilaterals.
SLIDE 29
A cyclic quadrilateral is any quadrilateral that can be inscribed within a circle.
Prove that the opposite angles of a cyclic quadrilateral add up to 180°.
SLIDE 30
Join each vertex of the quadrilateral to the centre of the circle O.
because they are all radii of the circle.
Each of the triangles are isosceles and angles that are equal are marked onto the diagram.
The angle sum of a cyclic quadrilateral is 360°.
The angle A is , the angle B is , so the sum of opposite angles is 180°.
SLIDE 31
The tangent to any curve is a straight line that just touches it.
The tangent to a circle is perpendicular to a radius.
Prove that the quadrilateral ABOC is a kite and show that it is also a cyclic quadrilateral.
SLIDE 32
The two triangles are mirror images of each other, so have identical sides.
and
It is a kite.
Since angles B and C are right angles, the sum of the other two angles in the kite must add to 180°, and ABOC is a cyclic quadrilateral.
SLIDE 33
ABCD is a cyclic quadrilateral where . Given that angle CDA is 70° and angle PAD is a right angle. Find the angle APC, marked x in the diagram.
SLIDE 34
Since ABCD is a cyclic quadrilateral, mark in the ex-circle.
PA is tangent to the circle, and so too is PC. That makes two right angles, as shown in the diagram.
Angle DOC is . AOCP is a kite, and angle AOC is . Since AOCP is also a kite, opposite angles add to 180°, which makes .
Alternative solution
Since , triangles OCP and OAP are identical. (We say they are congruent.) Triangles OCB and OAB are also congruent, and that makes all the angles y equal, as marked in red on the diagram. From there we can find the angles b and c, and then p.
|
|