|
Congruency |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Congruent triangles |
|
Workout |
|
35 slides |
|
| Congruency |
|
Library |
|
12 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Opposite, corresponding, alternating angles
|
|
600.1 |
|
|
Congruent triangles (identical triangles)
|
|
600.8 |
|
|
Sufficient condition
|
|
601.0 |
|
|
Necessary condition
|
|
601.2 |
|
|
ASA - sufficient condition of congruent triangles
|
|
601.6 |
|
|
SSS - sufficient condition of congruent triangles
|
|
601.7 |
|
|
SAS - sufficient condition of congruent triangles
|
|
601.8 |
|
|
SSA is not sufficient
|
|
602.0 |
|
|
RHS - sufficient condition of congruent triangles
|
|
602.2 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
Revision
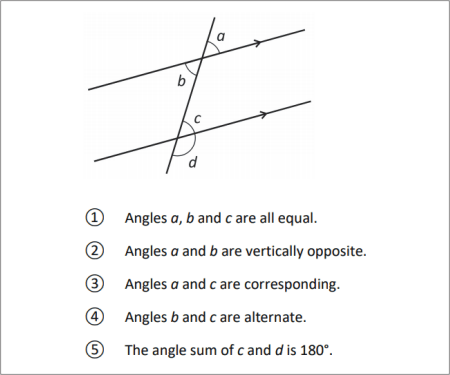
? Which angles in the diagram are equal?
? What is the name given to the relation between angles a and b?
? What is the name given to the relation between angles a and c?
? What is the name given to the relation between angles b and c?
? What is the angle sum of c and d?
SLIDE 2
? Angles a, b and c are all equal.
? Angles a and b are vertically opposite.
? Angles a and c are corresponding.
? Angles b and c are alternate.
? The angle sum of c and d is 180°.
SLIDE 3
Find the angle a
SLIDE 4
Triangle is isosceles as
a and d are alternating angles
SLIDE 5
Find the angle x.
SLIDE 6
The angle sum of a quadrilateral is 360°.
Therefore,
The two base angles of the isosceles triangle are equal.
Therefore,
SLIDE 7
What does it mean to say that two triangles are identical?
SLIDE 8
Congruent triangles
When are two triangles identical?
This question invites different answers.
One answer is that two triangles are identical if they exactly overlap each other. In other words, one triangle fits exactly on top of the other. Another way of putting this, is that the triangle is only identical to itself.
Another answer is that two triangles are identical if we could move one triangle so that it would fit exactly into the space occupied by the other. To make it clear what we mean, we say that the triangles are congruent.
SLIDE 9
Congruent triangles
Two triangles are congruent if we could move one triangle so that it would fit exactly into the space occupied by the other.
Must two triangles with exactly the same angles be congruent?
SLIDE 10
Two triangles are similar when their angles are equal. But one similar triangle may be larger than another.
Similarity is not a sufficient condition of congruency. Being similar does not make two triangles congruent.
SLIDE 11
“Two triangles are not similar, but they are congruent.”
Is this statement true or false?
SLIDE 12
If two triangles are not similar, then they can have at most one equal angle.
There is no way that one of these triangles can fit exactly into the space of the other. So, they cannot be congruent.
Therefore, similarity is a necessary condition of two triangles being congruent, but it is not a sufficient condition.
SLIDE 13
Necessary condition
A necessary condition is some fact that must be true in order to ensure some other fact. It is also called a precondition.
Example
If triangle A is congruent to triangle B, then triangles A and B must be similar. Similarity is a necessary condition of congruency. Similarity is a precondition of congruency.
SLIDE 14
Sufficient condition
A sufficient condition is a fact that if true ensures (forces) the truth of another fact.
Example
If two right angled triangles are both isosceles, then the two triangles must be similar.
It is a sufficient condition for two right angled triangles to be similar that they are isosceles.
Reason. A triangle contains a right angle. If it is also isosceles, the other two angles must be equal. As the angle sum of a triangle is 180°, the other two angles must be 45°.
SLIDE 15
We seek the sufficient conditions for when two triangles are congruent. Two triangles will be congruent when given information about one triangle, it is only possible to construct the second triangle in one way.
Example
? First triangle: you know the length of the base of a triangle, and the two angles on the base.
? Second triangle: is it possible to make a second triangle that is different from the first triangle?
Given the angles a and b, then, since the angle sum of a triangle is 180°, there is only one way to find third angle, c. This makes the two triangles similar. The size of the base, x, fixes the size of the whole triangle. Both triangles must be congruent.
The information allows us to construct the second triangle in only one way. We draw the base of length x and measure the two angles, a and b. Then, there is only one point of intersection, P, and only one way to construct the second triangle.
SLIDE 16
ASA
Two triangles are congruent if you know that two angles and the included side between the two angles are the same.
This is a sufficient condition for two triangles to be congruent. It is abbreviated to ASA, short for angle-side-angle.
In this abbreviation, the use of the letter A does not indicate that both angles are equal, as in an isosceles triangle.
The mention of the side being “included” is not really needed. The two triangles will also be congruent if the corresponding sides are equal.
SLIDE 17
SSS
Two triangles are congruent if you all three sides of both triangles are equal.
This is also another sufficient condition for two triangles to be congruent. It is abbreviated to SSS, short for side-side-side.
SLIDE 18
SAS
Two triangles are congruent if two sides are the same and the angle included between them is the same.
This is also another sufficient condition for two triangles to be congruent. It is abbreviated to SAS, short for side-angle-side.
SLIDE 19
SAS
Two triangles are congruent if two sides are the same and the angle included between them is the same.
This time the phrase “included” is needed. Show that if the angle is not included between two sides, then there generally are two different ways to construct a second triangle.
SLIDE 20
You are given two sides and an angle, but if you do not know that the angle is included within the two sides, then there are two ways to construct the triangle. Thus, SSA (side-side-angle) is not a sufficient condition for two triangles to be congruent.
SLIDE 21
We have shown that SSA is not sufficient when the angle is not included between the two sides. But there is one exception to this case.
Redraw the above diagram, but make the angle a right angle.
SLIDE 22
RHS
If the angle is a right angle, then even if the angle is not included between the two give sides, there is only one way to construct the triangle. The other side is the hypotenuse of a right-angled triangle.
This is abbreviated to RHS, right-hypotenuse-side.
SLIDE 23
Summary
Sufficient conditions for two triangles to be congruent
ASA
SSS
SAS
RHS
SLIDE 24
In each case state whether the two triangles are definitely congruent. If they are congruent, state the sufficient condition.
?
?
?
?
?
?
SLIDE 25
? Congruent
RHS
? Congruent
SSS
? Congruent
SAS
? Not congruent
? Not congruent
similar
? Congruent
ASA
SLIDE 26
Prove that ABO and DCO are congruent, and find the lengths of AB and OB.
SLIDE 27
The angles at O are vertically opposite. The angles at A and D are equal. ABO and DCO are congruent by ASA.
SLIDE 26B
Prove that ABO and DCO are congruent, and find the lengths of AB and OB.
SLIDE 27B
The angles at O are vertically opposite. The angles at A and D are equal. ABO and DCO are congruent by ASA.
SLIDE 28
Prove that ABO is congruent to DCO
SLIDE 29
The angles at O are vertically opposite. Between parallel lines, the other angles are alternating. The two parallel lines are equal, and corresponding sides. Therefore, ABO is congruent to DCO by ASA.
SLIDE 30
Triangle MPN is isosceles. Find the length of PO.
SLIDE 31
Since MPN is isosceles
In the triangles MPX and NPO, all three angles are equal, and MP corresponds to NP.
Therefore, MPX is congruent to NPO by ASA.
By Pythagoras,
SLIDE 32
In the quadrilateral ABCD, angle ABC is equal to angle BCD, and .
Prove that the diagonals, AC and BD are equal.
SLIDE 33
BC is common to both triangles ABC and DCB. We are given angle ABC is equal to angle BCD, and , so ABC and DCB are congruent by SAS.
Hence, AC and BD are equal.
SLIDE 34
Angles and are equal.
Prove that triangles ACF and GEB are congruent.
SLIDE 35
The angles x are equal (given). The angles y are equal because alternating and corresponding between parallel lines. , since AC and EG are parallel. Hence ACF is congruent to GEB by ASA.
(Alternative proofs are possible.)
|
|