|
The quadratic discriminant |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.5] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Consolidation - when a quadratic has no real roots
|
|
826.1 |
|
|
Imaginary and complex number
|
|
826.3 |
|
|
Discriminant
|
|
826.7 |
|
|
Discriminant criterion for 0, 1 (twice) and 2 roots
|
|
827.2 |
|
|
Application of discriminant criterion
|
|
827.3 |
|
|
Coefficient problem on discriminant, range of values
|
|
827.5 |
|
|
Coefficient problem on discriminant, second quadratic
|
|
828.0 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Discriminant
SLIDE 1
Consolidation
? Find the completed square form of and sketch its graph.
? Use the graph to state how many solutions there are to the equation .
? Attempt to solve using the quadratic formula. What problem do you encounter? How does this problem relate to the solution to the previous question?
SLIDE 2
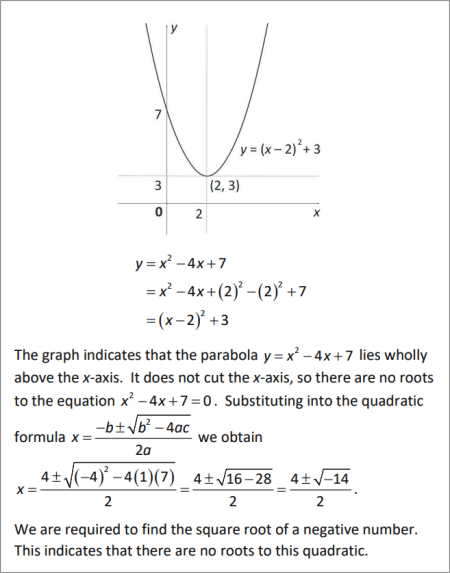
The graph indicates that the parabola lies wholly above the x-axis. It does not cut the x-axis, so there are no roots to the equation . Substituting into the quadratic formula we obtain . We are required to find the square root of a negative number. This indicates that there are no roots to this quadratic.
SLIDE 3
Real roots
Substituting into gives .
In any such situation where we encounter the square root of a negative number, we say that there are no real roots.
? What is a real number? What are real numbers used for?
? What does it mean to say that has no real roots?
Advanced
? We define the square root of a negative number to be an imaginary number, and any combination of a real and imaginary number to be a complex number. What kind of roots does have?
? The topic of imaginary and complex numbers lies outside the scope of this chapter.
SLIDE 4
? What is a real number? What are real numbers used for?
A real number is any number that can be used to measure such things as distances. Real numbers include both rational and irrational numbers. They are used to measure continuous quantities that we encounter in reality.
? What does it mean to say that has no real roots?
It means that any solution to the equation cannot be used to measure a real distance.
? We define the square root of a negative number to be an imaginary number, and any combination of a real and imaginary number to be a complex number. What kind of roots does have?
has complex roots involving an imaginary number. ? The topic of imaginary and complex numbers lies outside the scope of this chapter.
SLIDE 5
? Which part of the quadratic formula is square rooted?
? How could we arrive at the conclusion that has no real roots without substituting into the whole of ? Hint. For this purpose, we only need the part of the quadratic formula that is the answer to the first question.
SLIDE 6 – EXPLANATION AND SOLUTION
The part of this that falls under the square root symbol is . If this part is negative, then we know immediately that the quadratic equation has no real roots.
Example
As
SLIDE 7
Discriminant
Given the discriminant is defined to be
SLIDE 8
By computing the discriminant state whether each of the following has real roots or no real roots.
? ?
? ?
SLIDE 9
?
?
?
?
SLIDE 10
? Factorise and sketch its graph.
? What is the discriminant of ?
? How many solutions are there to ?
? What is the minimum of ?
? At how many points does the parabola meet the x-axis?
? How many roots does have?
SLIDE 11
?
?
? There is only one solution to , which is
? The minimum of is
? The parabola only meets the x-axis at one point, which is the minimum at
? Whether we count one or two roots to is a matter of definition. Mathematicians say that a function whose discriminant is 0, which touches the x-axis once, has one root repeated twice, or one root (twice). We say it has a repeated root because it has a repeated factor.
SLIDE 12
Note. When , you can also see the expression “equal roots” in place of “one real root twice”, or “one repeated root”.
SLIDE 13
How many solutions do the following equation have?
?
?
?
?
SLIDE 14
?
?
?
?
SLIDE 15
Example
Find the range of values of for the above equation to have a solution in the real numbers.
Note. the Greek letter “L” and is pronounced “lambda”.
Solution
SLIDE 16
For the following equations, find the range of the values of if there is to be a solution.
?
?
?
SLIDE 17
?
?
?
SLIDE 18
Show that for all values of , the equation has a solution.
SLIDE 19
Show that for all values of , the equation has a solution.
Solution
SLIDE 20
Find the values of k, which will ensure that has equal roots.
SLIDE 21
Find the values of k, which will ensure that has equal roots.
Solution
SLIDE 22
Show that always has solutions, for all values of .
SLIDE 23
Show that always has solutions, for all values of .
Solution
SLIDE 24
Find the set of possible values of k for which the equation has no real solutions for x.
SLIDE 25
Find the set of possible values of k for which the equation has no real solutions for x.
Solution
SLIDE 26
It is given that where p is a constant, has no real roots. Find the set of possible values of p.
SLIDE 27
It is given that where p is a constant, has no real roots. Find the set of possible values of p.
Solution
SLIDE 28
The equation , where q is a non-zero constant, has equal roots. Find the value of q.
SLIDE 29
The equation , where q is a non-zero constant, has equal roots. Find the value of q.
Solution
SLIDE 30
The equation , where k is a constant, has 2 different solutions for x. Find the set of possible values of k.
SLIDE 31
The equation , where k is an integer, has 2 different solutions for x. Find the set of possible values of k.
Solution
|
|