|
Quadratic inequalities |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Solving quadratic inequalities |
|
Workout |
|
33 slides |
|
| Quadratic inequalities |
|
Library |
|
12 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.2] |
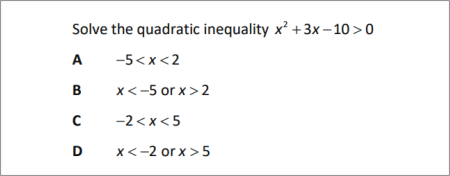 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Solving a quadratic inequality
|
|
822.3 |
|
|
Method of looking for change of sign
|
|
823.4 |
|
|
Manipulating quadratic inequalities
|
|
823.7 |
|
|
Geometric problem leading to quadratic inequality
|
|
823.9 |
|
|
Trap when quadratic inequality has rational denominator
|
|
824.3 |
|
|
Quadratics with rational denominator
|
|
824.5 |
|
|
Quadratics where denominator is always positive
|
|
824.6 |
|
|
Combining inequalities
|
|
824.8 |
|
|
Solving simultaneous quadratic inequalities
|
|
825.0 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Quadratic inequalities
SLIDE 1
Revision
Factorise . Hence find the roots of and sketch its graph.
SLIDE 2
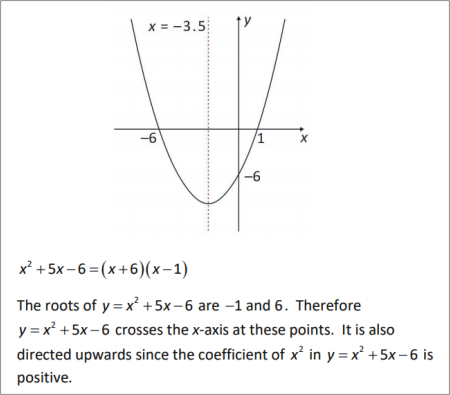
The roots of are . Therefore crosses the x-axis at these points. It is also directed upwards since the coefficient of in is positive.
SLIDE 3
Example
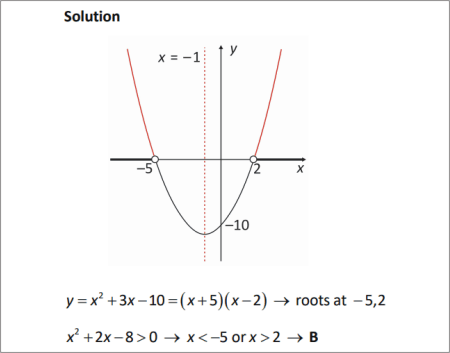
Solve the quadratic inequality
Solution
Sketch the graph of
The question asks us to find the values of x where the graph of the quadratic function lies above the x-axis. This graph lies above the x-axis when .
when .
SLIDE 4
Solve the quadratic inequality
SLIDE 5
SLIDE 6
Solve the quadratic inequality
SLIDE 7
SLIDE 8
Solve the quadratic inequality
SLIDE 9
SLIDE 10
Solve the quadratic inequality
SLIDE 11
SLIDE 12
Solve the quadratic inequality giving your answers to 3 significant figures.
SLIDE 13
SLIDE 14
Example
Solve by the method of looking for changes in the signs of factors.
Solution
interval
- + +
- - +
+ - +
SLIDE 15
Solve by the method of looking for changes in the signs of factors.
SLIDE 16
interval
- + +
- - +
+ - +
SLIDE 17
Solve
Hint
Recall that inequalities can be manipulated exactly like equations unless you multiply by (or any negative number). If you multiply by you reverse the sign of the inequality. Example, .
SLIDE 18
Following the hint, we can bring all terms to the left, as we are not multiplying by
SLIDE 19
The area of the rectangle is greater than the area of the triangle. Find the range of possible values of x.
SLIDE 20
The area of the rectangle is greater than the area of the triangle. Find the range of possible values of x.
Solution
SLIDE 21
The volume of the cone is greater than the volume of the hemisphere. Find the set of values of r, giving your answer in terms of exact surds of the form , where a and b are integers.
SLIDE 22
The volume of the cone is greater than the volume of the hemisphere. Find r.
Solution
It is an examiner trick to use a variable in a question that is also used in a formula. It is good practice to rewrite the formulas using a different symbol for the radius.
We substitute r for R in the first formula, also dividing by 2 to obtain the volume of a hemisphere; we substitute and 2r for h in the second formula.
SLIDE 23
A student is asked to solve
He argues as follows
? Substitute into . Why does this show that there must be an error in the student’s argument?
? There is a mistake in the student’s argument – what is it?
? Why is the statement included in the opening statement of the problem?
SLIDE 24 – EXPLANATION AND SOLUTION
? On substituting into we obtain
According to the above argument the solution set is supposed to include all of the interval , but here the statement is false for . Hence, there must be an error in the student’s argument.
? We are only allowed to step from to if the value of the denominator , for otherwise, we are multiplying by and we should reverse the sign of the inequality.
? is included because when the denominator is . We are never allowed to divide by 0.
SLIDE 25
Quadratics with rational denominators
? The solution to this type of problem lies outside the scope of this chapter.
However, the student should be aware that we can only multiply a denominator “up” to clear it from the bottom of a fraction if we know that it is a positive quantity.
SLIDE 26
? Explain why the denominator of is always positive.
? Hence, solve the inequality.
SLIDE 27
? The denominator of is . The square of any number is positive, hence .
? Hence, it is possible to solve this problem simply by multiplying the denominator up and off the bottom of the left-hand side.
SLIDE 28
Combining inequalities
Solve and
SLIDE 29
SLIDE 30
? Solve and .
? Sketch both and on the same diagram. Show in the diagram the solution set to the where and .
SLIDE 31
SLIDE 32
n is an integer such that and . Find the solution set for possible values of n.
SLIDE 33
n is an integer such that and . Find the solution set for possible values of n.
Solution
|
|