|
Completing the square |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Quadratics in canonical form |
|
Workout |
|
54 slides |
|
| Completing the square |
|
Library |
|
17 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - EXPLANATION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.2] |
 |
|
SOLUTION |
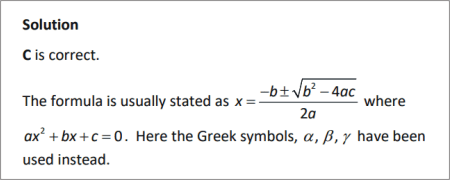 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Consolidation of the quadratic formula
|
|
784.1 |
|
|
The form μ(x - α)^2 + β
|
|
784.5 |
|
|
min / max at (α, β), axis of symmetry at x = α
|
|
784.7 |
|
|
The completed square
|
|
784.9 |
|
|
Canonical or standard form
|
|
784.9 |
|
|
Algebraic method for finding the completed square
|
|
785.0 |
|
|
Where ÎĽ < 0
|
|
785.2 |
|
|
Completing the square by direct manipulation
|
|
785.4 |
|
|
Plus/minus trick
|
|
785.4 |
|
|
Extending direct manipulation to fractions
|
|
786.1 |
|
|
Quadratic that does not have roots
|
|
786.7 |
|
|
Real roots
|
|
786.9 |
|
|
Square root of a negative number
|
|
787.0 |
|
|
Where x^2 coefficient is not unitary
|
|
787.5 |
|
|
Effect of ÎĽ on the parabola
|
|
787.8 |
|
|
Effect of ÎĽ < 0 on the parabola
|
|
788.2 |
|
|
Proof of the quadratic formula
|
|
788.4 |
|
|
Roots of a quadratic from the completed square
|
|
789.3 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Completing the square
SLIDE 1
Revision
?
State the quadratic formula to find the roots of the above equation.
? The graph of is a parabola. State the equation of the axis of reflective symmetry of this parabola.
SLIDE 2
Quadratic equation
Quadratic formula
Axis of reflective symmetry
This can be seen directly from the quadratic formula. The axis of symmetry lies midway between the two roots, and the formula gives the roots as .
SLIDE 3
? Solve .
? Find the equation of the axis of symmetry of the parabola , the minimum value, and sketch the parabola.
SLIDE 4
Axis of symmetry at
SLIDE 5
Note. is the Greek letter m, pronounced “mu” as in “music”.
? Expand and collect
?
Find the values of the constants .
? Substitute for in to obtain an equation for in the form
SLIDE 6
?
?
?
SLIDE 7
Axis of symmetry , minimum point
? State the relation between the axis of reflective symmetry of the parabola and the constants .
? State the minimum point of in terms of the constants .
SLIDE 8
Axis of symmetry , minimum point
? The axis of reflective symmetry is .
? The minimum point of is at
SLIDE 9
The completed square
Any quadratic function may be written in the form
This form is called the completed square for the quadratic function.
From this form, the axis of reflective symmetry of the parabola defined by is and its minimum or maximum is at .
The constant is the scale factor of the quadratic function.
If , then the parabola has a minimum.
If , then the parabola has a maximum.
Because the form makes all this information about the function and curve (parabola) transparent, it is called the standard or canonical form of the quadratic function.
SLIDE 10
Finding the completed square form
There are two methods for finding the completed square form – an algebraic method that we have already practised, and a method involving direct manipulation. The second method is more efficient, but we begin with the algebraic approach.
Algebraic method
It is given that .
? By expanding the right-hand side of this equation and equating coefficients, find the completed square form of
? State the axis of symmetry and minimum point of and sketch its parabola. (It is not required to find the roots.)
SLIDE 11
because the coefficient of is 1. This simplifies the working.
Equating coefficients
SLIDE 12
Find the completed square form of and sketch its parabola.
Hint. The negative coefficient of the quadratic term indicates that the parabola has a maximum.
SLIDE 13
SLIDE 14
Method of direct manipulation
The coefficient of the x term here is 5.
Half of this number is and the square of this is . Add and subtract simultaneously from the equation. (1, 2)
This step is called completing the square because .
Tidy up the “back end”.
1. Because we have added and subtracted we have really added 0, so the equation remains true. This is called a plus / minus trick.
2. Do not unsquare the first just after the 5x term, because it is the we want when we complete the square at the next step.
The method of direct manipulation is more efficient.
SLIDE 15
Find (by direct manipulation) the completed square form of and sketch its parabola.
SLIDE 16
SLIDE 17
Find the completed square form of and sketch its parabola.
SLIDE 18
SLIDE 19
Find the completed square form of and sketch its parabola.
SLIDE 20
SLIDE 21
Find the completed square form of and sketch its parabola.
Note. This problem extends the technique by involving fractions.
SLIDE 22
SLIDE 23
Find the completed square form of and sketch its parabola.
SLIDE 24
SLIDE 25
Find the completed square form of and sketch its parabola.
SLIDE 26
SLIDE 27
Find the completed square form of and sketch its parabola.
Remark. This graph of this quadratic function does not cross the x-axis.
SLIDE 28
SLIDE 29
Real roots
The quadratic function has completed square form with minimum . The graph of this function does not cross the x-axis, and the quadratic function does not have roots that are real numbers.
By completing the square, we can sketch a quadratic function that has no real roots. We have learnt earlier to sketch quadratic functions by finding their roots.
? Attempt to use the quadratic formula to find the roots of . What problem do you encounter? Why are you unable to find the roots of this quadratic function?
SLIDE 30
Using the quadratic formula
At this point we appear to arrive at an impasse, or impossible situation, as we encounter a negative square root.
The lesson we derive from this situation is that the process of completing the square is more versatile than the process of finding the roots of a quadratic function, as we can sketch the graph whether the function does or does not have real roots.
Advanced
Mathematicians define and declare a negative root to exist. By this means all quadratic functions can be factorised. This leads to the topic of complex numbers. The study of complex numbers occurs at a higher level.
SLIDE 31
Find the completed square form of and sketch its parabola.
Real roots
This parabola does not cross the x-axis, and the quadratic function does not have roots that are real numbers.
SLIDE 32
SLIDE 33
Find the completed square form of and sketch its parabola.
SLIDE 34
SLIDE 35
We now extend the method to the case where there is a coefficient in front of the quadratic term.
Example
Find the completed square form of .
Solution
The coefficient of the term here is 2
Take this coefficient outside the quadratic and linear terms, but not the constant term.
Inside the bracket add and subtract half the coefficient of the linear term.
Take the negative square outside the bracket, being careful to multiply by the coefficient outside the bracket.
Complete the square.
Tidy up the “back end”
SLIDE 36
Find the completed square form of and sketch its parabola.
SLIDE 37
SLIDE 38
Any quadratic function may be written in the form . The minimum of the graph of y is at .
The completed square form of is .
The minimum is at .
? What is the effect of the factor on the graph of y? How does affect or change the shape of the parabola?
SLIDE 39
In the effect of the scale factor is to change the “steepness” of the parabola. If then the parabola has everywhere (except for the turning point) a steeper gradient than the corresponding parabola where .
is “twice as steep” as
SLIDE 40
Find the completed square form of and sketch its parabola.
SLIDE 41
SLIDE 42
Find the completed square form of and sketch its parabola.
Note. The effect of is to “flip” the parabola – it has a maximum rather than a minimum.
SLIDE 43
SLIDE 44
Proof of the Quadratic Formula
The proof of the quadratic formula proceeds by completing the square. To demonstrate the formula all we follow through the steps of the previous exercises but with the parameters a, b and c in place of their values.
By completing the square on c, show that the solutions to the quadratic equation is given by
Note. Here we have added the subscripts 1, 2 to because generally there are two solutions to the quadratic equation. The formula is valid even if the expression equates to a negative square root.
We will take the proof in steps.
The coefficient of the term is a
? …. Take this coefficient outside the quadratic and linear terms, but not the constant term.
SLIDE 45
? …. Inside the bracket add and subtract the square of half the coefficient of the linear term.
SLIDE 46
? …. Take the negative square outside the bracket, being careful to multiply by the coefficient outside the bracket.
SLIDE 47
? …. Complete the square and simplify
SLIDE 48
? …. Tidy up the “back end”
SLIDE 49
? …. Take to the right-hand side.
SLIDE 50
? …. Take the square root of both sides of the equation. There can be positive and negative values.
SLIDE 51
? …. Simplify the right-hand side and bring to the right-hand side.
SLIDE 52
Proof of the quadratic formula
SLIDE 53
The completed square form of is
.
Use this information to solve the equation .
SLIDE 54
The completed square form of is
.
Use this information to solve the equation .
Solution
Reference
The coefficient of the term is a
Take this coefficient outside the quadratic and linear terms, but not the constant term.
Inside the bracket add and subtract half the coefficient of the linear term.
Take the negative square outside the bracket, being careful to multiply by the coefficient outside the bracket.
Complete the square and simplify
Tidy up the “back end”
Take to the right-hand side.
Take the square root of both sides of the equation. There can be positive and negative values.
Simplify the right-hand side and bring to the right-hand side.
Reference
|
|