|
Circles, curves and lines |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.6] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Circle locus, centre, radius, circumference
|
|
820.3 |
|
|
Radius of a circle and Pythagoras's theorem
|
|
820.6 |
|
|
Point on a circle
|
|
820.8 |
|
|
Equation of circle centre origin radius r
|
|
820.8 |
|
|
Reading centre and radius from r^2 = x^2 + y^2
|
|
821.1 |
|
|
Intersection of line and curve, graphical method
|
|
821.3 |
|
|
Intersection of line and curve, method of substitution
|
|
821.5 |
|
|
Centre of circle not the origin
|
|
822.1 |
|
|
General equation of circle centre C (a, b), radius r
|
|
822.5 |
|
|
Centre and radius of a circle from the general equation
|
|
822.8 |
|
|
Completing the square to find the general equation
|
|
823.0 |
|
|
Finding the radius of a circle through a given point
|
|
823.5 |
|
|
Circle and tangent problem
|
|
823.7 |
|
|
Showing a point lies on a circle
|
|
823.9 |
|
|
Circle and diameter problem
|
|
824.1 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
The equation of the circle etc
SLIDE 1
What are the defining properties of a circle?
Hint. To answer this question, ask yourself, how would you draw a circle? What would you need to draw a circle, and what makes a circle a circle, and not something else, such as a line, or another type of curve?
SLIDE 2
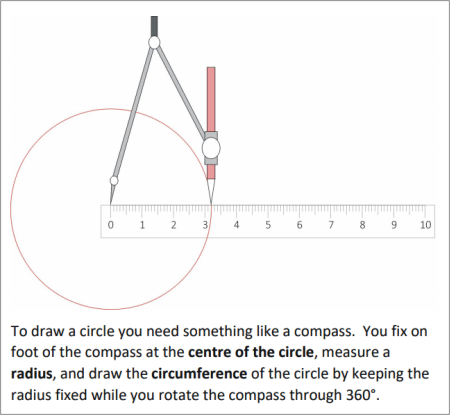
To draw a circle you need something like a compass. You fix on foot of the compass at the centre of the circle, measure a radius, and draw the circumference of the circle by keeping the radius fixed while you rotate the compass through 360į.
SLIDE 3
Defining properties of a circle
A circle has a centre, and fixed radius and a circumference. The circle (its circumference) is the path traced out by a point that travels 360į about the centre while keeping the radius fixed. We say that the circle (the circumference) is the locus of this point.
SLIDE 4
What is the centre and radius of this circle?
SLIDE 5
centre , radius 3
SLIDE 6
This circle has centre the origin and passes through the point .
? Use Pythagorasís theorem to find the exact radius of the circle.
? A point P on the circle has coordinates , where . Mark this point onto the diagram, and use your knowledge of the radius to find y.
SLIDE 7
? By Pythagorasís theorem the radius, r, of the circle is
? We have
Since , P has coordinates .
SLIDE 8
P is the point of a particle that is moving around a circle. Its coordinates are . Given that the radius of the circle is r, use Pythagorasís theorem to find an equation linking r, x and y, that holds (is true) regardless of where on the circle P lies.
SLIDE 9
We form a right-angled triangle, whose hypotenuse is the radius r. Then, by Pythagorasís theorem .
SLIDE 10
Equation of the circle, centre origin
The equation of the circle with radius r and centred on the origin is .
SLIDE 11
State the radius of the circle whose equation is
? ?
? ?
SLIDE 12
? ?
? ?
SLIDE 13
Draw onto the graph the circle with equation and the line with equation . Use the graph to find the coordinates of their point of intersection, giving your answer to the nearest 0.05.
SLIDE 14
is a circle or radius 3, centre the origin.
is a line with gradient and intercept 1.
The points of intersection are and to the nearest0.05.
SLIDE 15
? Make y the subject of equation (2)
? By substituting for y in (1), solve the system of equations and find their points of intersection, giving your answers to 2 decimal places.
SLIDE 16
?
? Substituting in
SLIDE 17
Draw onto the graph the circle with equation and the line with equation . Use the graph to find the coordinates of their point of intersection, giving your answer to the nearest 0.05.
SLIDE 18
is a circle or radius , centre the origin. is a line with gradient 2 and intercept . The points of intersection are and to the nearest 0.05.
SLIDE 19
Solve algebraically and .
SLIDE 20
SLIDE 21
? Find the centre and radius of this circle.
? Use Pythagorasís theorem to find the y-coordinate of the point whose x-coordinate is 3.6.
SLIDE 22
? The circle has centre and radius 5.
? To find the y-coordinate of the point whose x-coordinate is 3.6. We form a right-angle triangle, and find the length of the base. This is . By Pythagorasís theorem
The y-coordinate is
SLIDE 23
is a point on the circumference of a circle whose centre is and whose radius is r.
Find in terms of a, b and r, the equation of this circle, which is the same as the equation of the locus of P.
SLIDE 24
is the locus of a circle whose centre is and whose radius is r.
In the diagram, the base of the triangle is , the height of the triangle is . Substituting into Pythagorasís theorem in the form , we obtain as the general equation of a circle.
SLIDE 25
General equation of the circle
If is the locus of a circle whose centre is and whose radius is r , then the general equation of the circle is
Note. This form of the equation of the circle is also known as the Cartesian equation of the circle.
SLIDE 26
Find the Cartesian form of the equation of the circle with centre (?4, 3) and radius 5.
SLIDE 27
Find the Cartesian form of the equation of the circle with centre (?4, 3) and radius 5.
Solution
On substituting into , we obtain
SLIDE 28
Find the coordinates of the centre and the radius of the circles with the following equations.
?
?
?
?
?
SLIDE 29
?
?
?
?
?
SLIDE 30
Example
Find the centre and radius of the circle whose Cartesian equation is .
Method
We must complete the square in order to put the equation into the form . Once in this form we can read off immediately the centre and radius r.
Solution
SLIDE 31
Find the coordinates of the centre and the radius of the circle with equation .
SLIDE 32
Find the coordinates of the centre and the radius of the circle with equation .
Solution
SLIDE 33
Sketch the circle with the equation .
SLIDE 34
SLIDE 35
Find the equation of the radius joining the centre of the circle with equation to the point . Give your answer in the form , where a, b and c are constants.
SLIDE 36
Find the equation of the radius joining the centre of the circle with equation to the point .
Solution
We require the line joining the points and .
SLIDE 37
A circle is tangent to the x-axis and passes through the points and . Find the equation of the circle.
SLIDE 38
A circle is tangent to the x-axis and passes through the points and . Find the equation of the circle.
Solution
Since the circle is tangent to the x-axis, and touches it at , then it must be tangent to the x-axis at . This means that the centre of the circle lies on the line x = 6, at a point . Hence, . and lie on this circle.
SLIDE 39
The circle C has equation
? Find the centre and radius of C
? Show that the points and lie on C.
SLIDE 40
?
?
SLIDE 41
The circle C has equation with centre and radius 5. and lie on C.
? Show that PQ is a diameter of C
? R lies on the positive y-axis. Find the coordinates of R.
? Find the angle and the area of the triangle PRQ.
SLIDE 42
The circle C has equation with centre and radius 5. and lie on C.
?
. Since this is twice the radius, PQ must be a diameter of C.
? R lies on the positive y-axis
? Since PQ is a diameter, is a right-angle (circle theorem Ė angle subtended in a semicircle).
For the area of the triangle, the base is . The height is .
.
|
|