|
Algebraic products |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Products and expansions of polynomials |
|
Workout |
|
37 slides |
|
| Algebraic products |
|
Library |
|
15 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
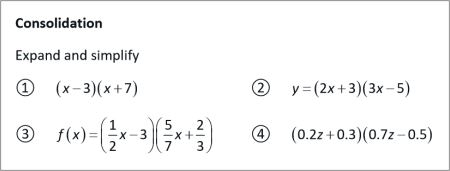 |
|
SLIDE 2 - SOLUTION |
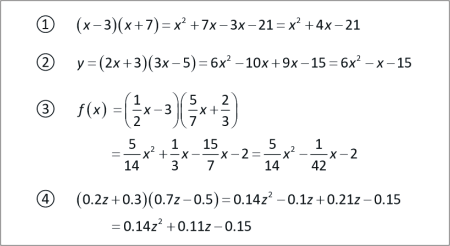 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
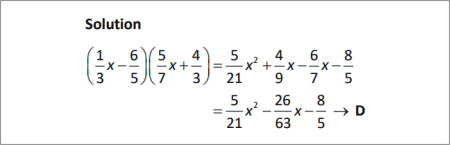 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Consolidation - expand and simplify binomial products
|
|
758.1 |
|
|
Consolidation of coefficient problem on products
|
|
758.5 |
|
|
Consolidation of equating coefficients problem
|
|
758.7 |
|
|
Expand and collect where one binomial, one trinomial
|
|
759.1 |
|
|
Simultaneous problem equating coefficients
|
|
759.4 |
|
|
Three product bionomial expansion
|
|
760.0 |
|
|
Method: factorising simple cubics
|
|
760.4 |
|
|
Expansions in higher powers
|
|
761.0 |
|
|
Multi-term expansions
|
|
761.2 |
|
|
From graph to polynomial problem
|
|
761.4 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Products and expansions
SLIDE 1
Consolidation
Expand and simplify
? ?
? ?
SLIDE 2
?
?
?
?
SLIDE 3
Simplify
SLIDE 4
SLIDE 5
Find
SLIDE 6
Find
Solution
SLIDE 7
, where a and b are constants.
Find the value of b.
SLIDE 8
, where a and b are constants.
Find the value of b.
Solution
SLIDE 9
, where a, b and c are constants. Find a, b and c.
SLIDE 10
, where a, b and c are constants. Find a, b and c.
Solution
SLIDE 11
Example
SLIDE 12
Expand and collect
? ?
SLIDE 13
?
?
SLIDE 14
where a, b and c are constants. Find the value of a, b and c.
SLIDE 15
where a, b and c are constants. Find the value of a, b and c.
Solution
SLIDE 16
where a and b are constants. Find the value of .
SLIDE 17
where a and b are constants. Find the value of .
Solution
SLIDE 18
where a, b and c are constants. Find the value of abc.
SLIDE 19
where a, b and c are constants. Find the value of abc.
Solution
SLIDE20
Example
Exercise
Expand and collect
? ?
? ?
SLIDE 21
?
?
?
?
SLIDE 22
Expand and collect
SLIDE 23
SLIDE 24
Factorising simple cubics
It is given that there are three factors of , and they have integer coefficients. Find the factors of .
Solution
We saw from the previous question that
Comparing the coefficients of the constant term and the quadratic terms we are looking for three integers such that
The prime factorization of 30 is . The possibilities are
Of these we have , so we have , and .
Check
SLIDE 25
Factorising simple cubics
where P, Q and R are integers. Factorise given than the factors have integer coefficients.
Method
Let the integer coefficients be a, b and c.
Equating coefficients
The three factors of times the constant term must sum to
the coefficient of the quadratic term.
You are looking for three factors of the constant term that add up to , where P is the coefficient of the quadratic term.
SLIDE 26
Given that the factors of have integer coefficients, factorise .
SLIDE 27
Given that the factors of have integer coefficients, factorise .
Solution
As the constant term is 10, we are looking for factors of .
The factors of are . As is a negative integer, one or three of the factors must be negative. As the coefficient of the is 2, we are looking for a sum of these integers that equates to . The possibilities are
, factors are
Check
SLIDE 28
Given that the factors of have integer coefficients, factorise .
SLIDE 29
. Given that the factors of have integer coefficients, factorise .
Solution
Constant term ? , Quadratic coefficient ? 2
Looking at factors of that sum to , where 0 or 2 are negative. The largest factor must be negative ? 2 negative.
Check
SLIDE 30
Which of the following is equivalent to ?
A
B
C
D
SLIDE 31
D
SLIDE 32
Expand and collect
?
?
?
SLIDE 33
?
?
?
SLIDE 34
The diagram shows a sketch of the graph of the cubic function where , A, B, C constant. Find .
SLIDE 35 Error in solution corrected – UPLOAD SLIDE
The diagram shows a sketch of the graph of the cubic function where , A, B, C constant. Find .
Solution
From the graph, the zeros (roots) of are . So, the factors are . Hence,
SLIDE 36
. Given that the factors of have integer coefficients, factorise and sketch the curve .
SLIDE 37
. Given that the factors of have integer coefficients, factorise and sketch the curve .
Solution
Constant term ? , Quadratic coefficient ? 4
Looking at factors of that sum to , where 0 or 2 are negative. The largest factor must be negative ? 2 negative.
Check
|
|