|
Trigonometric functions |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Graphs of trigonometric functions |
|
Workout |
|
54 slides |
|
| Trigonometric functions |
|
Library |
|
13 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - QUESTION 2 |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.5] |
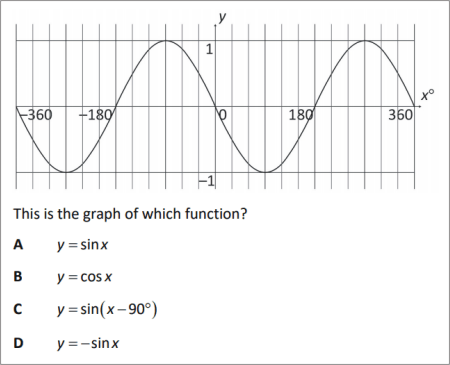 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Plotting and sketching grap of sin x
|
|
830.1 |
|
|
Consolidation - defining of six x for any angle
|
|
830.7 |
|
|
Sine wave
|
|
830.8 |
|
|
Periodic function
|
|
831.0 |
|
|
sin x is a periodic function
|
|
831.0 |
|
|
Period of sin x is 360 degrees
|
|
831.1 |
|
|
Two periods of the sine wave
|
|
831.2 |
|
|
sin x is infinitely many - one
|
|
831.6 |
|
|
arcsin not well defined unless the domain is restricted
|
|
831.9 |
|
|
Principal value of inverse sin
|
|
832.1 |
|
|
Solving θ = arcsin x
|
|
832.2 |
|
|
Vertical scaling of sin x
|
|
832.9 |
|
|
Reflection of sin x in the x-axis
|
|
833.1 |
|
|
Vertical translation of sin x
|
|
833.5 |
|
|
Horizontal translation of sin x
|
|
833.9 |
|
|
Generation of the sine wave
|
|
834.1 |
|
|
Generation of the cosine wave
|
|
834.2 |
|
|
Phase shift
|
|
834.3 |
|
|
Trigonometric identities
|
|
834.4 |
|
|
Phase shift trigonometric identities
|
|
834.4 |
|
|
Triangle trigonometric identities
|
|
834.5 |
|
|
Exact values of sin 30 sin 60 cos 30 cos 60
|
|
834.7 |
|
|
Using exact values of sin and cos in formulas
|
|
834.9 |
|
|
Exact values of sin 45 = cos 45
|
|
835.1 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Graphs of trigonometric functions
SLIDE 1
Use your calculator to complete the following table of values for the function . Give your answers to 2 decimal places.
0 30 45 60 90 120 135 150 180
0.71
210 225 240 270 300 330 345 360
SLIDE 2 - QUESTION
0 30 45 60 90 120 135 150 180
0.71 0.87 1 0.87 0.71 0.5 0
210 225 240 270 300 330 345 360
-0.5 -0.71 -0.87 -1 -0.87 -0.71 -0.5 0
Plot the points and sketch the graph of by joining the points with a smooth continuous curve with no “bumps”.
SLIDE 3
Some features of the graph of for
? It starts at 0 and cuts the x-axis at 180° and 360°.
? It has a maximum at and a minimum at
? The negative part is a reflection of the positive part, shifted along by 180°.
? Its value always lies between . It never takes a value outside this range.
SLIDE 4
How are angles measured in mathematics and geometry?
SLIDE 5
In geometry and mathematics angles are measured anti-clockwise from the direction pointing along the positive x-axis. This kind of angle is called an angle or circle measure.
SLIDE 6
How is defined for (a) an acute angle, (b) an obtuse angle and (c) a reflex angle?
SLIDE 7 - EXPLANATION
An acute angle lies in the first quadrant, an obtuse angle lies in the second quadrant, and a reflex angle lies in the third or fourth quadrants.
Taking the hypotenuse to be 1, which is possible because all trigonometric ratios are ratios in which the units of measurement cancel out, then in the first quadrant is the usual ratio , which given the unit hypotenuse, means that is the height of the triangle. In the second quadrant, is the mirror image of the values in the first quadrant, and likewise, in the third and fourth quadrants takes the same values as in the first and fourth quadrant, excepting that these are negative not positive, because they lie below the x-axis.
SLIDE 8 - EXPLANATION
Sine wave
The figure shows how the sine wave, , is generated for an angle . Note, here, the angle is and x represents the horizontal displacement of the triangle for a given angle . The value of is the height of this triangle measured relatively to the x-axis, so is positive above the x-axis and negative below it.
SLIDE 9
As circle measure is measured anti-clockwise from the positive x-axis, state without calculating the relationship between
? and
? and
? and
SLIDE 10
The sine wave is a periodic function
Circle measure is such that after a complete revolution of the angle comes back to the same place. If we are counting turns around the circle, then is one turn further along than , but if we are not counting turns then . (Whether we are counting turns around the circle or not, depends on the context of the question.) Hence is a periodic function such that . Every 360° the sine wave repeats itself. Hence, also
?
? and
? because
SLIDE 11
The period of the sine wave is 360°.
Draw two periods of the sine wave for .
SLIDE 12
SLIDE 13
Draw two periods of the sine wave for .
SLIDE 14
SLIDE 15
Is and one-one or a many-one function?
SLIDE 16 – EXPLANATION
Infinitely-many – one function
Since is a periodic function, for any given value of , there are infinitely many arguments of .
is an infinitely-many – one function, which is a characteristic of a periodic function.
SLIDE 17
Find , , and . Plot these points onto the sketch of .
SLIDE 18
SLIDE 19
? Why is a not well-defined function?
? How can we restrict the domain of , so that it has an inverse?
SLIDE 20
? a not well-defined function because is a many-one function, so for a given value of y we do not know which of the infinitely many arguments of to choose.
? We can restrict the domain of to a part where the function is one-one.
SLIDE 21
Principal value of inverse sine
The restriction of to the principal domain creates a one-one, increasing function which has a well-defined inverse, called the principal value of inverse sine.
.
SLIDE 22
Solving
We use our knowledge of the value of in the principal domain to find the solutions to in any required interval.
Example
Solve for , giving your answers to 0.1°.
The principal value of is
It is useful to make a sketch of the sine wave in the given interval. From the sketch we see that there are four solutions to the equation . These are
SLIDE 23
Solve for , giving your answers to 0.1°.
SLIDE 24
SLIDE 25
Solve for , giving your answers to 0.1°.
SLIDE 26
SLIDE 27
Revision – transformation of graphs
? On the same diagram sketch the graphs of and .
? How is the graph of obtained from the graph of ? (Alternatively, what is the relationship between the two graphs?)
? In general, what is the relationship between the graphs of and ?
SLIDE 28
The graph of is obtained from the graph of has a vertical scaling. For each argument of x the value of is twice the value of the corresponding value of .
The graph of is a vertical scaling by 2 of the graph of .
SLIDE 29
The figure shows a sketch of . Add to the figure a sketch of .
SLIDE 30
SLIDE 31
The figure shows a sketch of . Add to the figure a sketch of . Explain how the graph of is obtained from the graph of .
SLIDE 32
The graph of is obtained from the graph of by a scaling of scale factor 2 and a reflection in the x-axis.
SLIDE 33
Revision – vertical translation of a graph
? On the same diagram sketch the graphs of and .
? How is the graph of obtained from the graph of ?
? In general, what is the relationship between the graphs of and ?
SLIDE 34
The graph of obtained from the graph of by a vertical translation of .
In general, the graph of is obtained from the graph of by a vertical translation of .
SLIDE 35
The figure shows a sketch of . Add to the figure sketches of and . Explain how the graph of is obtained from the graph of .
SLIDE 36
The graph of is obtained from the graph of by a vertical scaling by scale factor followed by a vertical translation by .
SLIDE 37
Revision – horizontal translation of a graph
? On the same diagram sketch the graphs of and .
? How is the graph of obtained from the graph of ?
? In general, what is the relationship between the graphs of and ?
SLIDE 38
The graph of obtained from the graph of by a horizontal translation of in the positive x-direction.
In general, the graph of is obtained from the graph of by a horizontal translation of .
SLIDE 39
The figure shows a sketch of . Add to the figure a sketch of . How is the graph of obtained from the graph of ?
SLIDE 40
The graph of is obtained from the graph of by a horizontal translation of .
The value of in is called the phase shift of the sine wave.
SLIDE 41
The diagram shows how the sine wave is generated as the angle turns around a circle.
Use a similar approach to generate the cosine wave.
SLIDE 42
Generation of the cosine wave
SLIDE 43
The value of in is called the phase shift of the sine wave.
The figure shows the graphs of and . These graphs show that the graph of is identical to the graph of except for a phase shift.
Given and find .
SLIDE 44 - EXPLANATION
The graph of is identical to the graph of except for a phase shift of 90°.
and where .
indicates that the graph of can be obtained from the graph of by a horizontal translation of .
indicates that the graph of can be obtained from the graph of by a horizontal translation of .
Trigonometric identities
The expressions and are called trigonometric identities.
SLIDE 45
? Find x and y in terms of and .
? Find in terms of .
? By eliminating x, y and from your answers to part ? find identities for and .
SLIDE 46
?
?
?
SLIDE 47
Exact values
The trigonometric ratios have no units of measurements – they are just real numbers. Hence, the size of the triangle (its measured size) makes no difference to the ratio of the sides, and we are therefore “allowed” to chose sides of arbitrary length.
Triangle ABC is an equilateral triangle.
? Find
? Find
? Find
? Find exact values of , , and
SLIDE 48
Given ABC is an equilateral triangle
?
?
?
?
SLIDE 49
By substituting exact values, prove
SLIDE 50
, , ,
SLIDE 51
Use the above triangle to find the exact value of and .
SLIDE 52
SLIDE 53
Find the exact value of .
SLIDE 54
|
|