|
Recurrence relations |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Iterating a process |
|
Workout |
|
28 slides |
|
| Recurrence relations |
|
Library |
|
12 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.5] |
 |
|
SOLUTION |
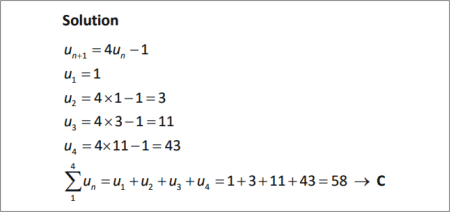 |
|
|
DEPENDENCIES |
|
|
|
320: Finding roots
|
|
|
| |  | | |
|
|
354: Recurrence relations |
|
|
| |  | | |
|
|
END OF COURSE
|
|
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Fixed point iteration (implicit)
|
|
820.3 |
|
|
Convergent, divergent, alternating sequence
|
|
821.1 |
|
|
Sigma notation for sum of terms
|
|
821.1 |
|
|
Recursion formula
|
|
821.3 |
|
|
Fibonacci sequence
|
|
821.5 |
|
|
Problems on recursion formulae
|
|
821.5 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
Show that is a rearrangement of .
SLIDE 2
Show that is a rearrangement of .
Solution
SLIDE 3
It is given that is a rearrangement of .
? Use the quadratic formula to solve . State the negative root, , of in an exact form in the form , where a and b are constants.
? Using the iterative formula , and starting with a value of find , giving your answers to 3 decimal places, where not exact.
? The sequence of iterations converges on a number . State the relationship between ?
SLIDE 4
?
?
? . converges on the root
SLIDE 5
? Using with , find the values of , giving your answers to 3 decimal places.
? Explain the relationship between and the equation .
SLIDE 6
?
? Since
is a rearrangement of . Hence are members of a sequence that converges on a root of .
SLIDE 7
? An approximate solution to an equation is found using the iterative formula . Starting with find , giving your answers to 6 decimal places
? Find the solution to , where , giving your answer to 5 decimal places.
SLIDE 8
?
?
Hence is an iterative formula converging on the negative root of . To find this root we must continue the sequence until it converges on to 5 decimal places.
SLIDE 9
? Show that is a rearrangement of
? Show that has a root , where .
? Using your answer to ?, write down an iterative formula that could be used to find this root . You may assume that this formula will give a convergent sequence.
? Starting with use the iterative formula of part ? to find to 5 decimal places. Write your values for to 7 decimal places.
SLIDE 10
?
?
? converges on .
?
SLIDE 11
? A sequence satisfies , where . Starting with find .
? State whether this sequence is convergent, divergent or alternating.
The symbol means “find the sum of all the terms in the sequence from .
? Evaluate .
SLIDE 12
?
? The sequence is divergent.
?
SLIDE 13
? A sequence satisfies , where . Starting with find .
? Given that , find .
? Evaluate .
SLIDE 14
?
?
?
SLIDE 15
The Fibonacci sequence is given by the recursion formula
? Given , find the first 7 terms of the Fibonacci sequence.
? Evaluate .
? Another sequence is defined by . Starting with , find the first 5 terms of this sequence.
SLIDE 16
?
The sequence is
?
?
SLIDE 17
? A sequence is defined by .
Find .
? Evaluate .
? Another sequence is defined by . Starting with , find the first 3 terms of this sequence.
? Prove that .
SLIDE 18
?
?
? .
? To prove that
SLIDE 19
A sequence is given by
Where k is an integer, .
? Find in terms of k, and
? Given that , find k.
SLIDE 20
?
?
SLIDE 21
A sequence is given by
Find the value of .
SLIDE 22
We begin by investigating the sequence
This is an alternating sequence, where for n odd, we have , and for n even we have . Since 1050 is even,
SLIDE 23
A sequence is given by
Give that , find the value of a.
SLIDE 24
Since we must find
SLIDE 25
For the sequence the terms are related by where . Find the value of State whether this sequence is convergent or divergent.
SLIDE 26
The sequence is divergent.
SLIDE 27
? .
? .
? Let be the difference between succussive terms of this sequence. forms another sequence such that the difference between successive terms is constant. Find the first term of sequence and the common difference. Prove that the common difference of this sequence is constant.
SLIDE 28
?
?
?
To prove that the common difference is constant
|
|