|
Geometry in three dimensions |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Thinking in three dimensions |
|
Workout |
|
32 slides |
|
| Geometry in three dimensions |
|
Library |
|
10 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - TASK 1 |
 |
|
SLIDE 2 - EXPLANATION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Compass
|
|
400.1 |
|
|
Circle - radius and centre (implicit locus)
|
|
400.2 |
|
|
Compass and ruler
|
|
400.3 |
|
|
Graph paper
|
|
400.4 |
|
|
Accurate
|
|
400.4 |
|
|
Point of intersection
|
|
400.4 |
|
|
Ruler and compass construction
|
|
400.6 |
|
|
Perpendicular bisector
|
|
400.6 |
|
|
Construction of an equliateral triangle
|
|
400.7 |
|
|
Construction of isosceles triangle
|
|
400.8 |
|
|
Construction of scalene triangle
|
|
400.8 |
|
|
Three-dimensional object
|
|
401.2 |
|
|
Regular tetrahedron
|
|
401.2 |
|
|
Net
|
|
401.3 |
|
|
Construction of a square
|
|
401.5 |
|
|
Bisection of an angle
|
|
401.7 |
|
|
Construction of a parallel line
|
|
401.9 |
|
|
Cube
|
|
402.1 |
|
|
Open box
|
|
402.3 |
|
|
Face (of a cube)
|
|
402.5 |
|
|
Opposite faces
|
|
402.5 |
|
|
Visualisation of three-dimensional object
|
|
402.9 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
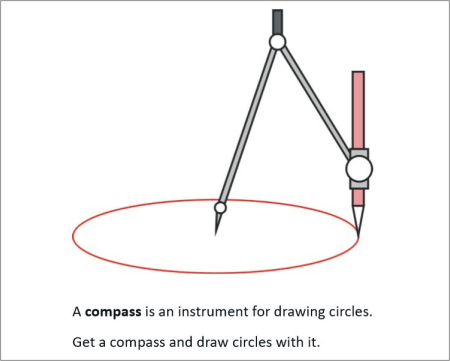
A compass is an instrument for drawing circles.
Get a compass and draw circles with it.
SLIDE 2
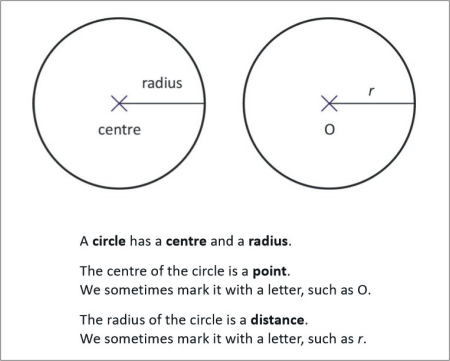
A circle has a centre and a radius.
The centre of the circle is a point.
We sometimes mark it with a letter, such as O.
The radius of the circle is a distance.
We sometimes mark it with a letter, such as r.
SLIDE 3
How to draw a circle using a compass and ruler.
Draw circles with radius: 3.2, 4.9 and 1.8 cm.
SLIDE 4
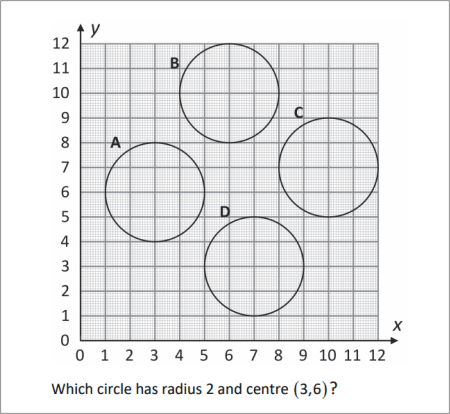
This is a circle with centre and radius 2.2.
This is positioned accurately on graph paper.
On the another piece of graph paper draw two circles accurately:
(a) centre , radius 2.5
(b) centre , radius 3.5
Find their points of intersection to the nearest 0.1.
SLIDE 5
Points of intersection:
SLIDE 6
Anything that can be made with a ruler and compass is a ruler and compass construction.
This is how to divide the line segment between two points A and B using a ruler and compass.
? Join the points A and B using a ruler.
? Draw a circle centred A with a radius larger than half the distance from A to B.
? Draw another circle with the same radius centred on B.
? Mark the two points of intersection, P and Q.
? Draw a line through P and Q.
The line PQ cuts AB at X.
X is midway between A and B. X is the midpoint of AB.
The line l joining P to Q is perpendicular to AB. It is the perpendicular bisector of AB.
The line l from P to Q is at right-angles to the line AB.
? Practise bisecting lines
SLIDE 7
This is how to construct an equilateral triangle using a ruler and compass.
? Draw a line of length r, which is the desired length of the base of the triangle.
? Set the compass to width r and draw two circles centred on the two end-points of the line.
? Join the end-points to the point of intersection.
What you have is an equilateral triangle. All the sides of the triangle are equal.
? Practise constructing equilateral triangles
? An isosceles triangle may constructed in a similar way. How?
SLIDE 8
Construction of an isosceles triangle
A scalene triangle is one with three different sides.
How does one construct a scalene triangle?
SLIDE 9
Construction of a scalene triangle
SLIDE 10
An equilateral triangle can be inscribed within a circle.
Construct an equilateral triangle and inscribe it in a circle.
SLIDE 11
? Construct the equilateral triangle
? Bisect one of the sides
? Bisect another of the sides to find the centre of the circle and confirm with bisecting the third side.
? Draw the circle touching the three vertices of the triangle
SLIDE 12
A regular tetrahedron is a three-dimensional object, where each side is an equilateral triangle.
Draw what you get if you cut the tetrahedron along three of its edges, open it out and lay it flat.
SLIDE 13
When you open out a tetrahedron you obtain a net.
Contract the net for a tetrahedron using a ruler and compass, add tabs so that the edges can be glued and make a tetrahedron.
SLIDE 14
SLIDE 15
Construct a square using ruler and compass
SLIDE 16
SLIDE 17
Construct a right-angle
Bisect this angle
Note
To bisect an angle means to divide the angle in two
SLIDE 18
SLIDE 19
Construct a line parallel to another line.
Note
Two lines are parallel if they are the same distance apart.
SLIDE 20
SLIDE 21
A cube is a six-sided three-dimensional object where each side is a square of the same size.
Construct an accurate net for a cube and make a cube.
SLIDE 22
SLIDE 23
Which of the nets could be used to make an open box?
SLIDE 24
The only net that will not make an open box is ? where two squares will overlap. These are shown in green.
In the other five examples, the base of the box is shown in pink.
SLIDE 25
A cube has six faces, each of which has a number.
The sum of the numbers on opposite faces is 7.
Draw the cube so that the three hidden faces can be seen.
SLIDE 26
Opposite sides adding to 7 are shown in the same colour.
SLIDE 27
SLIDE 28
SLIDE 29
Which of the following is the same object?
SLIDE 30
SLIDE 32
There are six matching pairs
SLIDE 33
|
|