|
Dimension and algebra |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
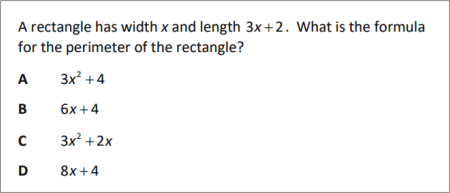 |
|
SOLUTION |
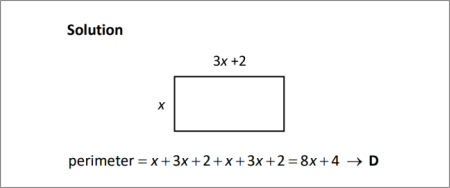 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Necessarily false
|
|
640.3 |
|
|
Dimension
|
|
640.5 |
|
|
Dimension of number, length, area, volume, time
|
|
640.7 |
|
|
Formulas for volume, surface area, perimeter of cuboid
|
|
640.9 |
|
|
Products of variables and dimension
|
|
641.3 |
|
|
Consistent dimensions
|
|
641.5 |
|
|
Alternative forms of Pythagoras's theorem
|
|
641.7 |
|
|
Consolidation of area formulas
|
|
641.9 |
|
|
Dimension of gradient
|
|
642.1 |
|
|
Dimensionless
|
|
642.2 |
|
|
Cross-ratio formula for similar triangles
|
|
642.3 |
|
|
Dimension of constant of proportionality
|
|
642.5 |
|
|
Hemisphere
|
|
643.3 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
SLIDE 1
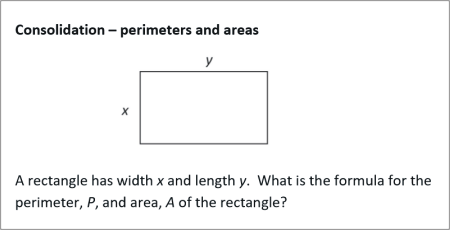
Consolidation Ė perimeters and areas
A rectangle has width x and length y. What is the formula for the perimeter, P, and area, A of the rectangle?
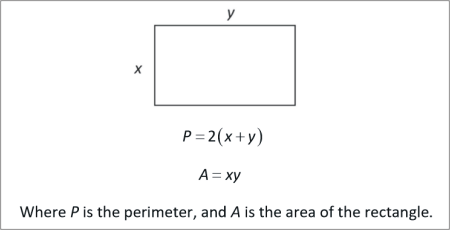
SLIDE 2
Where P is the perimeter, and A is the area of the rectangle.
SLIDE 3
The length of one side of a geometric shape is x cm. Someone claims that the area of the shape is . Why do we know that this statement is necessarily false?
SLIDE 4
The length of one side of a geometric shape is x cm. Someone claims that the area of the shape is . Why do we know that this statement is necessarily false?
Solution
If the length of one side of the shape is x cm, then is just adding 4 units that length, which is a length. No area can be made from a length simply by adding to that length another number.
The sum of a number and a length is a length. It cannot be anything else, such as an area or a volume.
SLIDE 3B
The length of one side of a geometric shape is x ft. Someone claims that the area of the shape is . Why do we know that this statement is necessarily false?
SLIDE 4B
The length of one side of a geometric shape is x ft. Someone claims that the area of the shape is . Why do we know that this statement is necessarily false?
Solution
If the length of one side of the shape is x ft, then is just adding 4 units that length, which is a length. No area can be made from a length simply by adding to that length another number.
The sum of a number and a length is a length. It cannot be anything else, such as an area or a volume.
SLIDE 5
The dimension of a length is 1
? What is the dimension of a length times a length?
? What is the dimension of the product of three lengths?
? What is the dimension of a number?
? What is the dimension of three lengths multiplied together and then multiplied by a period (of time)?
SLIDE 6
The dimension of a length is 1.
? The dimension of a length times a length is 2.
? The dimension of the product of three lengths is 3.
? The dimension of a number is 0.
? The dimension of three lengths multiplied together and then multiplied by a period (of time) is 4.
SLIDE 7
Let k be a number.
Let x, y and z be three lengths, and let t be a period (of time).
Complete the following table.
Formula Dimension Physical meanings
1 Line, length
SLIDE 8
Formula Dimension Physical meanings
0 Number
1 Line, length
2 Area
3 Volume
1 Period, duration
SLIDE 9
The dimensions of a cuboid are x, y and z. What are the formulas for the perimeter, surface area and volume of this cuboid?
SLIDE 10
SLIDE 11
What are the formulas for the perimeter, surface area and volume of a cube, when ?
SLIDE 12
SLIDE 13
Variables x, y and z represent three separate dimensions.
Any one variable represents a length.
The product of two variables represents an area.
The product of three variables represents a volume.
Classify the following as representing (a) a length, (b) an area, (c) a volume, or (d) none of these.
? ?
? ?
? ?
? ?
SLIDE 14
?
?
?
?
?
?
?
?
SLIDE 15
Consistent dimensions
In mathematics we can create an expression out of any variables. But an expression that represents an object with a dimension cannot be the sum of expressions with different dimension.
Example
consistent sum of three areas
inconsistent sum of a volume, an area and a length
In which of the following is the dimension consistent?
? ?
? ?
? ?
SLIDE 16
?
inconsistent sum of a volume, area and a length
?
consistent sum of three lengths
?
consistent sum of three areas
?
consistent product of a length and an area
consistent sum of three volumes
?
inconsistent sum of a volume and an area
?
inconsistent sum of a length and an area
SLIDE 17
Alternative forms of Pythagorasís theorem
?
?
For each of these expressions which of the following is correct?
A It is a relationship between volumes
B It is a relationship between areas
C It is a relationship between lengths
D It is a relationship between numbers, dimensionless
SLIDE 18
Alternative forms of Pythagorasís theorem
?
B It is a relationship between areas
?
C It is a relationship between lengths
SLIDE 19
Consolidation
Recall from memory, the formulas for the area of
? a triangle ? a parallelogram ? a trapezium
? a rhombus ? a kite
Draw a diagram for each.
SLIDE 20
? Triangle
? Parallelogram
? Trapezium
? Rhombus
and ? Kite
SLIDE 21
Dimension of gradient
The gradient of a line is the rise over the step.
While any letter may be used, it is customary to denote the gradient by m or k.
What are the dimensions of the gradient, m?
SLIDE 22
gradient
The units of the gradient are dimensionless. The gradient is just a number, and numbers have no dimension.
The gradient is the ratio of two lengths. When one length is divided by another, the units of measurement (length) cancel out, and we are left only with a number.
SLIDE 23
? Prove that triangle OPQ is similar to triangle ORS
? Find a formula connecting the numbers a, b, c and d.
Hint. Ratios in similar triangles are equal.
SLIDE 24
? Triangle OPQ is similar to triangle ORS because the angles at the centre are vertically opposite (x), and the other angles (for example, y) are corresponding angles between parallel lines.
? The ratio of corresponding sides in similar triangles are equal.
This ratio has several forms
SLIDE 25
The graph shows a relationship of direct proportionality between variables X and Y.
? Find the constant of proportionality, and the equation connecting X and Y.
? What are the dimensions of the constant of proportionality?
SLIDE 26
? Constant of proportionality
? The constant of proportionality is the gradient of the line, and is dimensionless.
SLIDE 27
Someone claims that the volume of a sphere is given by
Why must that person have made a mistake?
SLIDE 28
Someone claims that the volume of a sphere is given by
Why must that person have made a mistake?
Answer
There must be a mistake in this formula, because a volume has dimension 3, whereas the formula has dimension 2. The formula is for an area and not a volume.
SLIDE 29
Volume of a sphere
The formula for the volume of a sphere is in fact
? Explain why this formula has the right dimensions.
? Find the radius of a sphere that has the same volume as a cube of side 2 cm. Give your answer to 3 significant figures.
SLIDE 30
? Explain why this formula has the right dimensions.
The dimension of the formula is 3, which is the dimension of a volume.
? Find the radius of a sphere that has the same volume as a cube of side 2 cm.
Volume of cube is
SLIDE 29B
Volume of a sphere
The formula for the volume of a sphere is
? Explain why this formula has the right dimensions.
? Find the radius of a sphere that has the same volume as a cube of side 2 in. Give your answer to 3 significant figures.
SLIDE 30B
? Explain why this formula has the right dimensions.
The dimension of the formula is 3, which is the dimension of a volume.
? Find the radius of a sphere that has the same volume as a cube of side 2 in.
Volume of cube is
SLIDE 31
The volume of a sphere is . A lead ball has radius 3.2 cm and mass 1.55 kg. Find in the density of lead. Give your answer to 3 significant figures.
SLIDE 32
The volume of a sphere is . A lead ball has radius 3.2 cm and mass 1.55 kg. Find in the density of lead. Give your answer to 3 significant figures.
Solution
SLIDE 31B
The volume of a sphere is . A lead ball has radius 3.2 in and mass 56.4 lb. Find in the density of lead. Give your answer to 3 significant figures.
SLIDE 32B
The volume of a sphere is . A lead ball has radius 3.2 in and mass 56.4 lb. Find in the density of lead. Give your answer to 3 significant figures.
Solution
SLIDE 33
A bowl in the shape of a hemisphere of radius 25 cm is being filled with cream at a rate of per minute. How long will it take to fill the bowl to the brim? Give your answer to the nearest second.
The volume of a sphere is .
SLIDE 34
A bowl in the shape of a hemisphere of radius 25 cm is being filled with cream at a rate of per minute. How long will it take to fill the bowl to the brim? Give your answer to the nearest second.
Solution
The volume of the bowl is half the volume of a sphere with the same radius.
SLIDE 33B
A bowl in the shape of a hemisphere of radius 25 in is being filled with cream at a rate of per minute. How long will it take to fill the bowl to the brim? Give your answer to the nearest second.
The volume of a sphere is .
SLIDE 34B
A bowl in the shape of a hemisphere of radius 25 in is being filled with cream at a rate of per minute. How long will it take to fill the bowl to the brim? Give your answer to the nearest second.
Solution
The volume of the bowl is half the volume of a sphere with the same radius.
SLIDE 35
Two shapes, A and B, are similar. The ratio of the surface area of A to the surface area of B is . The volume of B is . Find the volume of A. Give your answer to 3 significant figures.
SLIDE 36
Two shapes, A and B, are similar. The ratio of the surface area of A to the surface area of B is . The volume of B is . Find the volume of A.
Solution
The ratio of the side or radius of the shape will be as the square root of the ratio of the surface areas. The volume will in the ratio of the cube of the side or radius.
SLIDE 35B
Two shapes, A and B, are similar. The ratio of the surface area of A to the surface area of B is . The volume of B is . Find the volume of A. Give your answer to 3 significant figures.
SLIDE 36B
Two shapes, A and B, are similar. The ratio of the surface area of A to the surface area of B is . The volume of B is . Find the volume of A. Give your answer to 3 significant figures.
Solution
The ratio of the side or radius of the shape will be as the square root of the ratio of the surface areas. The volume will in the ratio of the cube of the side or radius.
|
|