|
Quadratics |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Quadratic roots |
|
Workout |
|
42 slides |
|
| Quadratics |
|
Library |
|
18 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
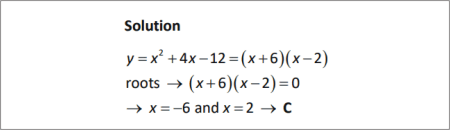 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Consolidation of quadratic factorisation and roots
|
|
716.1 |
|
|
Harder quadratic factorisation with integer coefficients
|
|
716.9 |
|
|
Harder quadratic factorisation with surds as roots
|
|
717.6 |
|
|
Quadratics without integer factors
|
|
718.0 |
|
|
Relationship between factors and roots
|
|
718.2 |
|
|
Not all quadratic functions have roots
|
|
718.4 |
|
|
Vertical translation of the parabola
|
|
718.4 |
|
|
The form ax^2 + bx + c
|
|
718.6 |
|
|
The quadratic formula
|
|
718.8 |
|
|
Axis of symmetry of parabola at x = - b/2a
|
|
719.3 |
|
|
Volume problems leading to a quadratic
|
|
720.1 |
|
|
Tricky business of formula terms reused as variables
|
|
720.2 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Quadratics
SLIDE 1
Consolidation
Factorise and find the roots of
? ?
? ?
SLIDE 2
?
?
?
?
SLIDE 3
? Sketch the graph of
? Summarise the properties of a quadratic curve
SLIDE 4
?
? A quadratic curve is a parabola. It is symmetric about a vertical axis of symmetry and has either a minimum or a maximum point. If it cuts the x-axis, then these points are the roots of the quadratic function. The parabola cuts the y�-axis at an intercept.
SLIDE 5
Sketch the graph of
SLIDE 6
SLIDE 7
Example
Exercise
Factorise and find the roots of
? ?
? ?
SLIDE 8
?
?
?
?
SLIDE 9
Example
Factorise
Solution
We must look simultaneously at pairs of factors of both the and the units coefficients, which are 4 and 6 respective.
We must consider every possible combination of these pairs of factors
A middle x coefficient of is possible when
We check this by multiplying out the proposed solution
?
SLIDE 10
Factorise the following and find the roots
? ?
? ?
SLIDE 11
?
?
?
?
SLIDE 12
Sketch the graph of
SLIDE 13
SLIDE 14
Sketch the graph of
SLIDE 15
Pairs of factors of 150 are
We observe , so we expect the factors of 150 to be 5 and 30, with 7 multiplied by 5.
SLIDE 16
Example
Factorise
Solution
Check ?
Exercise
Factorise the following, check your answers, and find the roots
? ?
? ?
SLIDE 17
?
?
?
?
?
?
?
?
SLIDE 18
It is given that
? Find the roots of this function as exact numbers and as decimal approximations to 2 decimal places.
? What kind of numbers are the exact roots?
? Find the minimum of the graph of .
? Sketch the graph of .
SLIDE 19
?
Roots at
? These are irrational (or real) numbers. They are not exact fractions or integers.
? Axis of symmetry at
At minimum
SLIDE 20
Quadratics without integer factors
cannot be factorised using integers
Proof. The only possible factors of 1 are , but , so it is not possible to add or subtract these factors to obtain the coefficient of x, which is 1.
Exercise
Three of the following six quadratic functions cannot be factorised with integers. Identify which they are and factorise those that can be factorised.
? ?
? ?
? ?
SLIDE 21
?
?
?
?
?
?
SLIDE 22
Relationship between factors and roots
quadratic function factors roots
Find the quadratic functions in the form that have the roots
? ?
? ?
SLIDE 23
?
?
?
?
SLIDE 24
Not all quadratic functions have factors and roots
The graph of is the standard parabola.
The graph of is obtained from the graph of by a vertical translation of the parabola by +1.
? On the same diagram sketch the graphs of and .
? Use the sketch to explain why has no factors or roots.
SLIDE 25
The graph of lies above the x-axis, and never crosses it. The roots correspond to those points on the x-axis where the parabola crosses it. Hence has no roots, and has no factors either.
SLIDE 26
When a quadratic function is written , the coefficient of the term is a, the coefficient of the x term is b and the coefficient of the units is c.
Complete the following table
a b c
1 3 4
SLIDE 27
a b c
1 3 4
1 6 1
2 -5 -3
-1
7
SLIDE 28
The quadratic formula provides a method of finding roots of quadratic functions. If then the roots are given by
We will prove this formula in a higher-level chapter. For now, we learn to use it.
Example
Find the roots of , giving your answer to 3 sf.
Solution
. Substituting into
SLIDE 29
Quadratic formula
If then the roots are given by
Use the quadratic formula to find the roots of the following, giving your answers to 3 significant figures
? ?
SLIDE 30
?
?
SLIDE 31
If then the roots are given by
Use the quadratic formula to find the roots of the following, giving your answers to 3 significant figures
? ?
SLIDE 32
?
?
SLIDE 33
If , then the axis of symmetry of the parabola is at .
Find the axis of symmetry of the parabolas of the following quadratic functions
? ?
? ?
SLIDE 34
?
Axis of symmetry at
?
Axis of symmetry at
?
Axis of symmetry at
?
Axis of symmetry at
SLIDE 35
Quadratic formula
If then the roots are given by
Axis of symmetry of a parabola
If , then the axis of symmetry of the parabola is at .
Use the quadratic formula to find the roots of , and sketch the curve.
SLIDE 36
Axis of symmetry
When
SLIDE 37
is a quadratic.
Write down from memory ? the quadratic formula for the roots of y, ? the equation of the axis of symmetry of the parabola defined by y.
SLIDE 38
Quadratic formula
If then the roots are given by
Axis of symmetry of a parabola
If , then the axis of symmetry of the parabola is at .
SLIDE 39
Use the quadratic formula to find the roots of , and sketch the curve.
SLIDE 40
Axis of symmetry
When
SLIDE 41
The volume of the sphere and the volume of the cone are equal. Form a quadratic equation and use the quadratic formula to find r, giving your answer to 2 decimal places.
SLIDE 42
The volume of the sphere and the volume of the cone are equal. Form a quadratic equation and use the quadratic formula to find r, giving your answer to 2 decimal places.
Solution
The formulas for the volume of a sphere and a cone are
It is a standard trick of examiners designed to expose any confusion in the student, to use in a question a variable that is the same letter as in a standard formula. So, we must change the variable r in the formulas to something else, such as R
We substitute into the left-hand formula, and into the right-hand formula, while equating the volumes.
A negative solution is not possible,
|
|