|
Functions |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Functions, inverse and composition |
|
Workout |
|
45 slides |
|
| Functions |
|
Library |
|
17 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
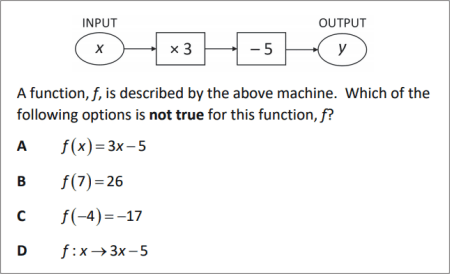 |
|
SOLUTION |
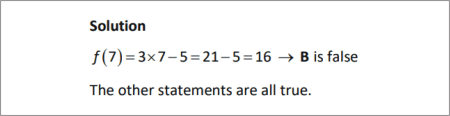 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Inverse of a function
|
|
732.3 |
|
|
Inverse function notation
|
|
732.3 |
|
|
Identity of functions independent of variable used
|
|
732.4 |
|
|
Transposing to find the inverse of a function
|
|
732.8 |
|
|
Switching the variable in the inverse function problem
|
|
732.8 |
|
|
Problems on simple number machines
|
|
733.1 |
|
|
Inverse of the function f(x) = (ax + b) / (cx +d)
|
|
733.9 |
|
|
Composition of functions, chain
|
|
734.1 |
|
|
Composing functions, fg(x) = f(g(x))
|
|
734.4 |
|
|
Identity function f(x) = x
|
|
734.7 |
|
|
Inverse the inverse of a function, ff^(–1) = 1
|
|
734.8 |
|
|
Simplying with rule ff^(–1) = 1
|
|
734.9 |
|
|
Product of functions
|
|
735.1 |
|
|
Distinction between products and chains
|
|
735.1 |
|
|
Resolution of ambiguity in the symbol fg
|
|
735.1 |
|
|
Composition of functions is not order invariant
|
|
735.2 |
|
|
Commutative operation
|
|
735.4 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Functions
SLIDE 1
Functions
A function is a process that takes an input number and produces an output number. A function may be thought of as a machine for computing an output for a given input.
Some functions are represented by a simple number machine.
The input is also called the argument and the output is called the value for the given argument.
A function may also be represented by a rule. The rule for the above number machine is
? Find the value of the above function for and .
? Find and
SLIDE 2
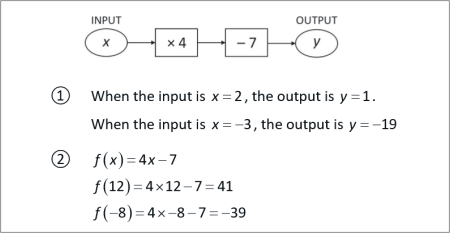
? When the input is , the output is .
When the input is , the output is
?
SLIDE 3
The inverse of a function
For functions that can be represented by a simple number machine, the inverse function may be represented by reversing the arrows in the machine diagram.
Above is the simple number machine of the function . By reversing the arrows, the inverse of has the simple number machine
The inverse of a function is written . This is said, “f inverse”, and not “f to the minus 1”. The inverse of this function is .
? For , find
? State the difference, if there is any, between the following
(a) and
(b) and
(c) and
SLIDE 4
?
? (a) and
The only difference is in the choice of letter to represent the input. But the rule is the same. In other words, these are the same function.
(b) and
(c) and
The same point applies to both the above cases. The only difference is in the choice of letter to represent the input. But the rule is the same. In both cases, the same function is represented.
SLIDE 5 This should be identity of functions – spelling error corrected here. CHECK THE SLIDE
Identity of functions
Two functions are identical if they have the same rule. In other words, the choice of letters to represent both the function and the variable make no difference to the function.
For example, , and are all one and the same function.
SLIDE 6
There are four pairs of identical functions in the following list.
Find all the pairs, and the two functions that are not identical.
? ?
? ?
? ?
? ?
? ?
SLIDE 7
? ?
? ?
? ?
? ?
?
?
SLIDE 8
Example
A function is defined by . Make x the subject of and hence find the inverse of .
Solution
Notes to this solution
In the last step we replace the variable y by the original variable x. This is a standard device required in most examinations to demonstrate understanding that the two functions and are one and the same function. The same result can be obtained by switching the variables at the beginning and writing as the line after .
SLIDE 9
Find the inverse
? ?
SLIDE 10
? ?
SLIDE 11
When the two inputs are equal, show that the difference between the outputs is always 14.
SLIDE 12
When the two inputs are equal, show that the difference between the outputs is always 14.
Solution
Machine 1
Machine 2
Difference of outputs is
SLIDE 13
When the two outputs are equal, show that the second input is always larger than the first input.
SLIDE 14
When the two outputs are equal, show that the second input is always larger than the first input.
Solution
Since we require the outputs to be equal, we must first invert both machines.
Machine Rule Rule for inverse
1
2
Equating , the difference of inputs is
SLIDE 15
Fill in the missing entries
function graph mapping
SLIDE 16
function graph mapping
SLIDE 17
Revision
Transpose for x.
SLIDE 18
SLIDE 19
Find the inverse of
? ?
SLIDE 20
?
?
SLIDE 21
Composition of functions
g and f are two machines: and .
By making the output of g into the input of f, we create a new machine, which is g followed by f.
The new function g followed by f is written . Note that the order of the functions f and g in is the reverse of the letters f and g in “g followed by f”. The rule for , from the mapping diagram, is .
SLIDE 22
? Find
? What is ?
? Find
? Find and simplify
SLIDE 23
?
?
?
?
SLIDE 24
Composing functions
This is read, “ of x is f of g of x”.
This is the same as g followed by f applied to x.
Example
If and , find .
Solution
Remark
When composing functions according to the rule , we work from the inside to the outside. That is, we begin by substituting into and then apply f to that value.
If then .
SLIDE 25
Find
? ?
? ?
? ?
SLIDE 26
?
?
?
?
?
?
SLIDE 27
The identify function is
The identity function makes no change to the input. It leaves the input identical to itself. The identity function is sometimes written 1 or e.
SLIDE 28
Inverse of an inverse
The composition of any function with its inverse is the identity function.
Example
Simplify
Solution
SLIDE 29
Simplify
? ?
? ?
? ?
SLIDE 30
?
?
?
?
?
?
SLIDE 31
Find in terms of x
SLIDE 32
Find in terms of x
Solution
Machine 1
Machine 2
SLIDE 33
What is the value of ?
SLIDE 34
What is the value of ?
Solution
SLIDE 35
If what is x?
SLIDE 36
If what is x?
Solution
SLIDE 37
g h
2 17
3 j
j k
In the table above, if find k
SLIDE 38
g h
2 17
3 j
j k
In the table above, if find k
Solution
SLIDE 39
f and g are functions such that and
? Find
? Find
SLIDE 40
f and g are functions such that and
?
?
SLIDE 41
Products and chains
Suppose and .
? The composition of g followed by f is
The composition of two functions is also called a chain.
? The product of f and g is
Ambiguity
The symbol is potentially ambiguous because it could indicate either of two different processes. It could indicate a composition of functions or a chain of functions.
Strictly, the symbol indicates a composite (chain) of functions. When a product is required, the symbol is used. However, occasionally, and even in exam papers, the symbol is used when a product is intended. The context makes it clear which is meant.
Where one wishes to be clear that a composition (chain) is mean the symbol is used: is an alternative to .
Note, it is not advisable it use the symbol for a product of functions, because at a higher level it is used it indicate something else.
SLIDE 42
Let and .
? Find and .
? Find and
? What do you observe in the second case that you do not find in the first?
SLIDE 43 missing space before f(x) corrected CHECK SLIDE
Let and .
? Composition (chain)
? Product
? We observe that . The order in which we multiply functions together makes no difference to the outcome. This is because the order in which we multiply numbers makes no difference to the product. However, here . The order in which we compose functions in general makes a difference to the outcome: g followed by f is not in general the same as f followed by g.
Note. Sometimes it may happen that .
SLIDE 44
An operation is commutative if the order in which the two of these operations produces the same output.
Which of the following operations is commutative?
? Product (multiplication)of numbers
? Sum (addition) of numbers
? Product (multiplication) of functions
? Composition (chain) of functions
SLIDE 45
? Product (multiplication)of numbers is commutative
Example
? Sum (addition) of numbers is commutative
Example
? Product (multiplication) of functions is commutative
Example
? Composition (chain) of functions is not commutative
Example
|
|