|
Systems of linear equations |
|
|
|
To use the resources of this chapter you must first register |
|
|
CONTENTS |
|
|
ITEM |
|
TYPE |
|
NUMBER |
|
| Lines and systems of equations |
|
Workout |
|
48 slides |
|
| Systems of equations |
|
Library |
|
12 questions |
|
|
|
Once you have registered, you can work through the slides one by one.
The workout comprises a series of sides that guide you systematically through the topic concept by concept, skill by skill. The slides may be used with or without the support of a tutor. The methodology is based on problem-solving that advances in logical succession by concept and difficulty. The student is presented with a problem or series of questions, and the next slide presents the fully-worked solution. To use the material you must sign-in or create an account.
blacksacademy.net comprises a complete course in mathematics with resources that are comprehensive.
|
|
|
|
SAMPLE FROM THE WORKOUT |
| Showing American English version |
SLIDE 1 - QUESTION 1 |
 |
|
SLIDE 2 - SOLUTION |
 |
|
|
SAMPLE FROM THE LIBRARY |
| Showing American English version |
QUESTION [difficulty 0.1] |
 |
|
SOLUTION |
 |
|
|
DEPENDENCIES |
|
|
|
|
CONCEPTS |
|
|
|
|
LEV. |
|
|
Relationship between gradient and graph of a line
|
|
744.7 |
|
|
Finding the equation of a line through two points
|
|
745.1 |
|
|
Consolidation of the method of elimination
|
|
745.8 |
|
|
System of equations with no solution
|
|
746.1 |
|
|
Coefficient problem in a system with no solution
|
|
746.3 |
|
|
System of equations with infinitely many solutions
|
|
746.7 |
|
|
Problem on identity of equations
|
|
746.8 |
|
|
Coefficient problem in a system with infinite solutions
|
|
747.0 |
|
|
Rotation of a line clockwise by 90 degrees
|
|
747.2 |
|
|
Criterion for perpendicular lines, m1 × m2 = –1
|
|
747.6 |
|
|
Distance problem in coordinate geometry
|
|
748.3 |
|
|
Ratio problem on straight line
|
|
748.5 |
|
|
|
|
RAW CONTENT OF THE WORKOUT |
|
| To make use of this chapter, please first register. Then you can work through the slides one by one. |
|
| What is provided here is the raw text of the workout. Most of the information is contained in the image files, which are not included with this text. The text may appear deceptively short. (The content overall of blacksacademy.net is vast.) Any in-line questions appear as a question mark [?]. This text is provided only as an indication of the overall quantity of material contained in the chapter. To use the material you must sign-in or create an account. |
|
| * |
|
|
Systems of linear equations
SLIDE 1
Revision
SLIDE 2
SLIDE 3
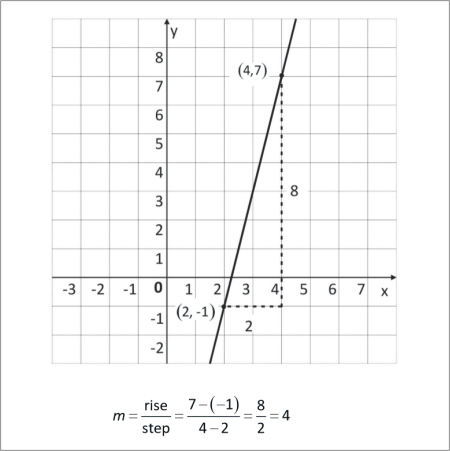
The symbol means “a change in”. The expression stands for a change in y. The gradient of a line may be written
The context makes it clear what kind of change is meant. Here the change in y is the rise, and the change in x is the step.
A line goes through two points with coordinates and . Find in terms of these coordinates.
SLIDE 4
SLIDE 5
? By substituting into the equation find the gradient of the line which passes through the points and .
? Sketch the line.
? How can we tell from the slope of a graph whether the gradient is positive or negative?
SLIDE 6
A line which is upward sloping has a positive gradient. A line which is downward sloping has a negative gradient.
SLIDE 7
Draw onto one diagram three lines passing through the origin with gradient m such that ? ? ? . Describe in words the slope of each line.
SLIDE 8
?
?
?
SLIDE 9
Draw onto one diagram three lines passing through the origin with gradient m such that ? ? ? . Describe in words the slope of each line.
SLIDE 10
?
?
?
SLIDE 11
The equation of the straight line is where m is the gradient and c is the intercept on the y-axis.
Example
Find the equation of the straight line that passes through the points .
Solution
Sub into
Sub into
Solve for c
SLIDE 12
Find the equation of the line passing through the points and . Sketch the line.
SLIDE 13
SLIDE 14
Find the equation of the line passing through the points and . Sketch the line.
SLIDE 15
SLIDE 16
Find the equations of the lines passing through the points
? and
? and
SLIDE 17
? and
? and
SLIDE 18
Consolidation
Solve by the method of elimination the simultaneous equations
By rearranging both equations as or otherwise, make a sketch of both lines illustrating the solution.
SLIDE 19
SLIDE 20
? Sketch on a single diagram the two lines joining
? For each, find the equation of the line, their intercepts and their gradients.
? What is the relationship between the two lines? Why can’t there be a simultaneous solution?
SLIDE21
Their gradients are the same, and they differ only in their intercepts. Because they are parallel lines, there cannot be a point of intersection between the two lines, so there cannot be a simultaneous solution to the two equations.
SLIDE 22
Criterion for no solutions to a system of simultaneous equations
A system of two simultaneous solutions has no solution if the lines represented by the two equations are parallel, while having different intercepts on the y-axis.
Example
Find the number of solutions to the above system of equations.
Solution
Rearrange both equations in the form
The gradients of both equations are the same. They are parallel lines. They have no solutions. Number of solutions is 0.
SLIDE 23
? This system of equations has no solutions. Given that a and b are constants, what is the value of ?
? What are the values of a and b when the two equations are the same equation?
SLIDE 24
? This system of equations has no solutions. Given that a and b are constants, what is the value of ?
? What are the values of a and b when the two equations are the same equation?
Solution
? ?
SLIDE 25
In the system of equations above, a is a constant. This system has no solutions. What is the value of a?
SLIDE 26
In the system of equations above, a is a constant. This system has no solutions. What is the value of a?
Solution
If they have no solutions, then they are parallel lines that differ in at most the intercept. The ratio of the y-coefficients in the two equations is . Multiplying by 3.4
. Hence, .
Note. We can also rearrange both equations in the form and equate the gradients.
SLIDE 27 – error “parallel” in second line changed to “identical” CHECK SLIDE.
Criterion for infinitely many solutions to a system of simultaneous equations
A system of two simultaneous solutions has infinitely many solutions if the lines represented by the two equations are identical
Example
These have infinitely many solutions because when the second equation is multiplied by 4 and rearranged, we obtain the first equation. .
Remarks
They have infinitely many solutions because the two lines “overlap”, and hence “overlap” at infinitely many places.
The expression “infinitely many solutions” is a façon de parler (French for “manner of speaking”). Since the two lines are identical, then in one sense there is only one equation, and only one line. Strictly, there is no system of equations. But in another sense, there is a system, because two things are given or written down. The expression “infinitely many solutions” is a disguised way of asking the student to recognise that one equation is a multiple of the other.
SLIDE 28
In the above, two of the equations are the same. Which are they?
SLIDE 29
Equations are the same equation.
SLIDE 30
In the system of equations above, m and n are constants. The system has infinitely many solutions. Find the ratio of m to n.
SLIDE 31
In the system of equations above, m and n are constants. The system has infinitely many solutions. Find the ratio of m to n.
Solution
Infinitely many solutions ? the two equations are identical. Since , we obtain .
Hence,
The ratio .
Note. If we are prepared to take it on trust that the two equations are the same (without checking it), then the ratio is automatically the ratio of the x and y coordinates in the second equation, because they are the same equation ?
SLIDE 32
Duplicate of questions from work out 273, chapter 272, level 6.1
? Rotate the triangle 90° clockwise about the point . Find the gradient of the hypotenuse.
? Draw the line passing through the points and . Find the gradient of this line.
? Draw the line perpendicular to the line you have just drawn passing through . What is the gradient of this perpendicular line?
SLIDE 33
The gradient of the line PQ is .
The line that is perpendicular to PQ has the same gradient as the triangle that has been rotated 90°. The gradient is .
SLIDE 34
? In terms of , what is the gradient, , of the line ?
? Rotate the triangle 90° clockwise about the point P. Mark the line made by the hypotenuse of this rotated triangle and find in terms of , what is the gradient, , of this line.
? Find the product of the two gradients, .
SLIDE 35
SLIDE 36
Criterion for when two lines are perpendicular
Two lines are perpendicular when the product of their gradients is equal to .
SLIDE 37
Perpendicular
? Make the subject of the above equation
? State in words what is in terms of ?
SLIDE 38
Perpendicular
?
? is the negative reciprocal of .
SLIDE 39
State whether the following pairs of lines are (a) parallel, (b) perpendicular or (c) neither parallel nor perpendicular.
? ?
? ?
? ?
SLIDE 40
?
?
?
?
?
?
SLIDE 41
These two linear equations define lines that are
A parallel and different
B perpendicular
C neither perpendicular nor parallel
D parallel and the same
E both parallel and perpendicular
SLIDE 42
Rearranging the second equation
The gradients are the same, the intercepts are different.
Solution
A parallel and different
SLIDE 43
The points and are 8 units apart on the same line. Find x.
SLIDE 44
The points and are 8 units apart on the same line. Find two possible values of x.
Solution
This is an application of Pythagoras’s Theorem.
We are not told whether x is greater than or less than 9, so there are two possibilities – the lie is upward sloping or downward sloping.
?
?
The two possible values of x are and .
SLIDE 45
Square are drawn under a line as shown in the figure. Find the coordinates of P.
SLIDE 46
As they are squares, we can find the gradient of the line, .
Let the side of the third square be s. By similar triangles
The coordinates of the point Q in the figure are , so the coordinates of P are .
SLIDE 47
The equation of the line QRV is . The gradient of the line PRT is twice the gradient of the line QRV. Find the ratio of PQ to RS.
SLIDE 48
The equation of the line QRV is . The gradient of the line PRT is twice the gradient of the line QRV. The coordinates of T are . Find the ratio of PQ to RS.
Solution
The gradient of line PRT is
To find R,
|
|